P3369 普通平衡树的一种非常规做法复盘：不使用 Treap / Splay，而是用 01Trie 维护有序多重集合。

前言

这篇文章记录我做 洛谷 P1637 三元上升子序列 和 SPOJ INCSEQ Increasing Subsequences 的过程，以及中途无意间发现的一套可以 通解“长度为 k 的严格上升子序列计数” 的模板。

大致路线：

1. 先从 P1637 出发，用两棵树状数组把“三元上升子序列”写成一个非常自然的过程；
2. 再把这套写法抽象成数学形式，发现它其实已经是一个“按长度分层 + 按值域前缀和”的 DP 框架；
3. 在 SPOJ INCSEQ 上把这个框架推广到「任意 k」，整理成一份可以直接丢进代码库的模板。

第一部分：P1637 三元上升子序列（k = 3）

1. 题面

Luogu P1637 三元上升子序列

信息提炼：

• 目标是统计三元组

  $$(i, j, k)\quad \text{s.t. } i < j < k,\ a_i < a_j < a_k$$
• $1 \le n \le 3\times 10^4$，值域很大，需要离散化；

• 朴素 $O(n^3)$ 显然不行；

• 即使是 “枚举中点 j，然后往左往右扫” 的 $O(n^2)$ 也过不了。

所以需要一个 $O(n\log n)$ 级别的写法。

2. 思路：按“长度”分层，而不是按“左右”切

很多三元上升子序列的题解会强调：

• 左边有多少个比 $a_j$ 小（记作 $L[j]$）；
• 右边有多少个比 $a_j$ 大（记作 $R[j]$）；
• 答案 = $\sum_j L[j]\cdot R[j]$。

我事先并不知道这种题解里的标准做法，没有这么写，而是直接按“子序列的长度”来分层维护：

• 长度为 1 的上升子序列：$(i)$
• 长度为 2 的上升子序列：$(i, j)$，满足 $i < j,\ a_i < a_j$
• 长度为 3 的上升子序列：$(i, j, k)$，满足 $i < j < k,\ a_i < a_j < a_k$

从左到右扫描下标 pos，当前值为 a[pos] = p 时，分三步：

1. 把当前值当成第三个元素 $k$
   • 统计所有“以前已经形成的、结尾值 < p 的长度为 2 的上升子序列”的数量；
   • 这些序列都可以接上 $p$，变成长度为 3 的上升子序列；
2. 把当前值当成第二个元素 $j$
   • 统计所有“结尾值 < p 的长度为 1 的上升子序列”的数量；
   • 这些和 $p$ 组成长度为 2 的上升子序列；
3. 把当前值当成第一个元素 $i$
   • 自身是一个长度为 1 的上升子序列。

这背后的数学形式可以抽象成两组函数：

• $f_1(v)$：长度为 1、结尾值为 $v$ 的严格上升子序列个数；
• $f_2(v)$：长度为 2、结尾值为 $v$ 的严格上升子序列个数。

对当前值 $p$（离散后下标为 $idx$），有：

整体答案就是所有“长度为 3 的新增数量”的累加。

问题变成：如何高效支持“按值域求 $\sum_{u < p} f_\ell(u)$”——典型的前缀和 + 单点更新场景，直接上树状数组。

3. 离散化 & 两棵树状数组

3.1 值域离散化

因为 $a_i$ 值域不小，直接拿它做 BIT 下标不稳妥，先做离散化：

1. 把所有 a[i] 放进 disperse；
2. 排序 + 去重；
3. 对每个 a[i] 找到它在 disperse 中的下标（从 1 开始），记作 idx。

之后所有树状数组下标都用这个 idx。

3.2 两棵 Fenwick Tree 的含义

代码中我开了两棵树：

• cnt_op
  • 维护 $f_1(v)$，即“长度为 1 的上升子序列”的计数；
  • 其实就是当前位置之前值为 $v$ 的元素出现次数；
• double_pair
  • 维护 $f_2(v)$，即“长度为 2 的上升子序列”的计数；
  • 记录所有以值 $v$ 结尾的长度为 2 的上升子序列有多少个。

于是：

• $\sum_{u < p} f_1(u)$ 可以写成 query(idx - 1, cnt_op)；
• $\sum_{u < p} f_2(u)$ 可以写成 query(idx - 1, double_pair)。

4. 扫描过程 & “从前往后滚”的正确性

对每个 p，离散下标 idx，按顺序执行：

1. 当前作为第三个元素 $k$

1

ans += query(idx - 1, double_pair);

2. 当前作为第二个元素 $j$

1

update(idx, query(idx - 1, cnt_op), double_pair, (ll)disperse.size());

3. 当前作为第一个元素 $i$

1

update(idx, 1, cnt_op, (ll)disperse.size());

整个过程是从左到右扫描、从“长度 2”再到“长度 1”更新，看上去好像会担心“当前元素更新的结果被自己读到”。
但注意：

• 所有 query 用的是 idx - 1；
• Fenwick 的实现保证 query(idx - 1) 只会访问 index < idx 的位置；
• 而 update(idx, ...) 写的是 index ≥ idx 的节点。

所以，无论是二维（P1637 的 f1/f2）还是推广到 k 维（后文），从前往后滚完全不会读到当前元素刚写入的那一格，不存在污染问题。

5. P1637 最终 AC 代码

代码完全按我自己的写法保留，用 vector + 离散化 + 两棵 Fenwick。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll maxn = 3e4 + 5;

ll n, ans;
vector<ll> a, disperse;

ll lowbit(ll x) {
    return x & -x;
}

void update(ll x, ll add, vector<ll> &tree, ll limit) {
    for (ll i = x; i <= limit; i += lowbit(i)) {
        tree[i] += add;
    }
}

ll query(ll x, vector<ll> &tree) {
    ll sum = 0;
    for (ll i = x; i; i -= lowbit(i)) {
        sum += tree[i];
    }
    return sum;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    a.reserve(maxn);
    disperse.reserve(maxn);
    cin >> n;
    for (ll i = 1; i <= n; ++i) {
        ll num;
        cin >> num;
        a.push_back(num);
        disperse.push_back(num);
    }
    sort(disperse.begin(), disperse.end());
    disperse.erase(unique(disperse.begin(), disperse.end()), disperse.end());
    vector<ll> double_pair(disperse.size() + 5, 0);
    vector<ll> cnt_op(disperse.size() + 5, 0);
    for (ll p: a) {
        ll idx = lower_bound(disperse.begin(), disperse.end(), p) - disperse.begin() + 1;
        ans += query(idx - 1, double_pair);
        update(idx, query(idx - 1, cnt_op), double_pair, (ll) disperse.size());
        update(idx, 1, cnt_op, (ll) disperse.size());
    }
    cout << ans;
    return 0;
}

（一些做题时的草稿）

到这里，P1637 这道 k=3 的问题就解决了。下面进入本文的重点：如何把这套写法推广到任意 k，并整理成模板。

第二部分：从 P1637 到通用 k 阶模板 —— INCSEQ 实战

这一部分主要做三件事：

1. 用数学形式把上面的 P1637 写法彻底抽象；
2. 在此基础上推广到任意长度 $k$；
3. 用 SPOJ INCSEQ 这道典型题来验证模板，并给出最终代码。

1. 抽象 P1637 的 DP 结构

先把 P1637 的写法抽象出来。

对离散后的值域 $[1, m]$，对所有长度 $\ell \ge 1$，定义

在 P1637 中：

• $f_1(v)$ 存放在 cnt_op 这棵树；
• $f_2(v)$ 存放在 double_pair 这棵树；
• 每一轮扫描时，会新增一部分“长度为 3”的数量并累加到 ans，但不显式存 $f_3(v)$。

对当前元素值 $p$（下标 idx），转移可以统一写成：

如果我们愿意把 $f_3$ 也显式地存下来，那么：

于是自然得到一个对于任意 $\ell \ge 2$ 的统一公式：

这就是“按长度分层做 DP，按值域用 Fenwick 求前缀和”的核心结构。

2. 推广到任意 k：通用递推公式

对于一般的“长度为 k 的严格上升子序列计数”，我们希望在处理完所有元素之后得到：

转移规则推广为：

每一层对应一个 Fenwick 树：

• 第 $\ell$ 层的 Fenwick 维护 $f_\ell(v)$ 在值域上的前缀和，因此

  $$\sum_{u < v} f_{\ell-1}(u) = \text{Fenwick}\_{\ell-1}.query(\text{idx}-1)$$

如果换成“数组写法”的 DP 形式，设

那么同样的转移可以写成：

再用 Fenwick 把右侧的“前缀和”这一项压缩到 $O(\log m)$ 即可。

3. 这里为什么也可以“从前往后滚”？

注意上面的循环顺序（对应我的 INCSEQ 代码）：

1
2
3
4
5
6
7

for (ll p: a) {
    int idx = ...;
    for (int i = 2; i <= k; ++i) {
        update(idx, query(idx - 1, dp_tree[i - 1]), dp_tree[i], size);
    }
    update(idx, 1, dp_tree[1], size);
}

和很多 DP 不同，这里完全不需要从 k → 1 逆序，原因有两点：

1. 对固定的 len，我们读取的是上一层 dp_tree[len - 1]，
   这一层在当前元素 p 的循环中，还没有被更新过；
2. 即使在“长度维度”上有前后依赖（例如 len=3 依赖 len=2），
   由于我们只查询 query(idx - 1, dp_tree[len - 1])，
   而当前元素的新贡献只写在 idx 及其后的节点上，
   所以这部分新贡献不会被读到。

Fenwick 树的结构保证：

• update(idx, ...) 只写 index ≥ idx 的节点；
• query(idx - 1) 只读 index ≤ idx - 1 的节点。

因此：
从前往后 len=2..k 滚动是绝对安全的，每一层用到的永远都是“上一层在当前元素之前的状态”。

4. 把模板落地：SPOJ INCSEQ

SPOJ INCSEQ - Increasing Subsequences

题目大意：给定 $n$、$k$ 和一个长度为 $n$ 的序列，统计长度恰好为 k 的严格上升子序列个数，对 MOD = 5,000,000 取模。
约束大致为：

• $1 \le n \le 10^4$
• $1 \le k \le 50$
• $0 \le a_i < 100000$

与我们抽象出的模型完全一致，非常适合作为模板题。

5. 实现细节解读

结合我自己的 AC 代码，这里的关键点有几个：

5.1 离散化

仍然通过 coord 进行排序 + 去重，把原始值映射到 $[1, size]$：

1
2
3
4

sort(coord.begin(), coord.end());
coord.erase(unique(coord.begin(), coord.end()), coord.end());
int size = (int) coord.size();
int idx = (int) (lower_bound(coord.begin(), coord.end(), p) - coord.begin()) + 1;

这样 Fenwick 的大小只需与 size 相关，而不受原值域限制。

5.2 k 层 Fenwick 的组织方式

使用一个二维数组：

1

vector<vector<ll> > dp_tree(k + 5, vector<ll>(size + 5, 0));

这里的含义是：

• dp_tree[len] 是“长度为 len 的那一层 Fenwick 树内部数组”；
• dp_tree[len][pos] 就是 $f_\ell(v)$ 在树状数组上的内部节点。

配合 update / query 函数，这就形成了 k 层树状数组结构。

5.3 模运算

代码里所有加法都通过

1
2

tree[i] = (tree[i] + val) % MOD;
sum = (sum + tree[i]) % MOD;

保持在 $[0, \text{MOD})$ 内，防止溢出；
同时题目需要对 5,000,000 取模，这里直接在 Fenwick 的每一步更新里处理掉。

5.4 复杂度

对于每个元素 p：

• 需要对 len = 2..k 做一次 query + update，每次是 $O(\log size)$；
• 再对 len = 1 做一次 update。

整体时间复杂度：

在 $n = 10^4, k \le 50$ 的条件下是完全没压力的。

6. INCSEQ 最终 AC 代码

这份代码是我在 SPOJ 上 AC 的版本，用的正是上面抽象出的模板思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll maxn = 1e4 + 5, MOD = 5000000;

ll n, k;
vector<ll> a, coord;

int lowbit(int x) {
    return x & -x;
}

void update(int idx, ll val, vector<ll> &tree, int limit) {
    for (int i = idx; i <= limit; i += lowbit(i)) {
        tree[i] = (tree[i] + val) % MOD;
    }
}

ll query(int idx, const vector<ll> &tree) {
    ll sum = 0;
    for (int i = idx; i; i -= lowbit(i)) {
        sum = (sum + tree[i]) % MOD;
    }
    return sum;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    a.reserve(maxn);
    coord.reserve(maxn);
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) {
        ll num;
        cin >> num;
        a.push_back(num);
        coord.push_back(num);
    }
    sort(coord.begin(), coord.end());
    coord.erase(unique(coord.begin(), coord.end()), coord.end());
    int size = (int) coord.size();
    vector<vector<ll> > dp_tree(k + 5, vector<ll>(size + 5, 0));
    for (ll p: a) {
        int idx = (int) (lower_bound(coord.begin(), coord.end(), p) - coord.begin()) + 1;
        for (int i = 2; i <= k; ++i) {
            update(idx, query(idx - 1, dp_tree[i - 1]), dp_tree[i], size);
        }
        update(idx, 1, dp_tree[1], size);
    }
    cout << query(size, dp_tree[k]);
    return 0;
}

（另一些做题时的草稿）

总结：可以直接收进代码库的结论

用一句话概括这篇文章要留下的东西，就是这组状态转移：

如果换成数组写法，设

则等价的 DP 形式是：

再用 Fenwick 把右侧的「前缀和」这一项压缩到 $O(\log m)$，就得到一套：

• 时间复杂度 $O(n\cdot k \cdot \log n)$；
• 支持任意 $k$ 的严格上升子序列计数；
• 可以轻松套在不同题目上的通用模板。

P1637 是这套模板在 $k=3$ 情况下的“特例写法”；
INCSEQ 则是把这个结构完整展开的一道标准模板题。

后面如果再遇到“长度为 k 的严格上升子序列”相关题目，可以直接在这份代码基础上做修改和扩展，而不需要重新从头推思路。

前言

这一次的 CF1065 C1/C2，是一对非常具有代表性的 XOR 博弈题。

在比赛当时，这两题看上去像是在操作数组、模拟交换，但真正的本质来自一个非常稳定的结构：

• 一个在整个游戏过程中保持不变的整体异或 T
• 一个决定双方 XOR 大小关系的最高有效位（msb）
• 以及一个能改变局势的“最后的关键下标”

C1 是单 bit 游戏，C2 是多 bit 游戏，但二者的本质高度统一，甚至 C2 可以视为 C1 的自然推广。

文章会以“复盘 + 结构化分析”的方式来讲：

• C1：理解最简 XOR 博弈（0/1）
• C2：推广到 general XOR 博弈（≤10⁶）
• 最后给出整个 XOR 博弈体系的总结

期间也会穿插 ASCII 示意图，帮助理解关键下标、最高有效位等结构。

下面进入正文。

C1. Renako Amaori and XOR Game (Easy Version)

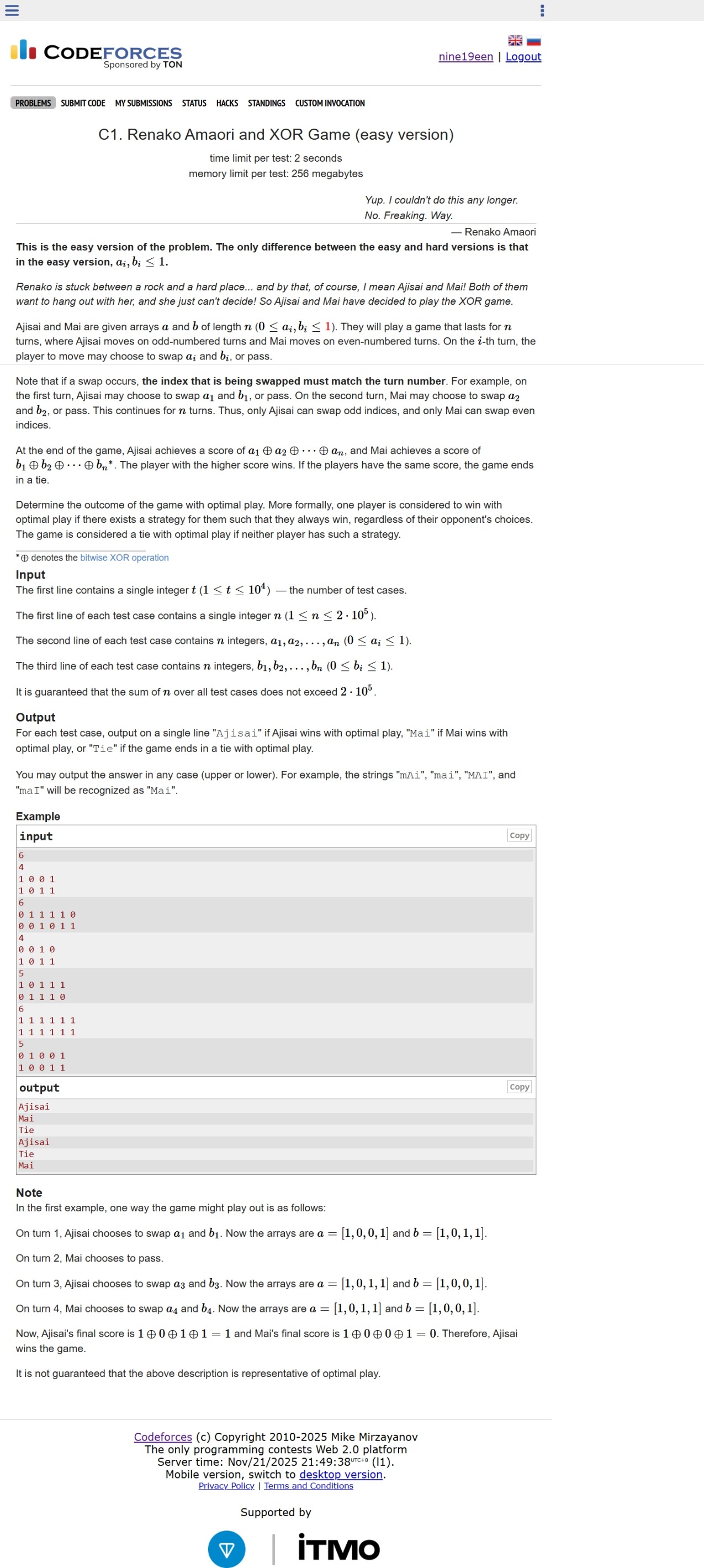
题面

题目翻译

给定两个长度为 n 的数组 a 与 b，其中所有元素均为 0 或 1。
游戏共进行 n 回合：

• 若 i 为奇数，则由 Ajisai 操作；
• 若 i 为偶数，则由 Mai 操作。

在第 i 回合，操作者可以选择：

• 交换 a[i] 与 b[i]，或
• 什么也不做（pass）

游戏结束后，评分如下：

• Ajisai 的分数为：a[1] ⊕ a[2] ⊕ ... ⊕ a[n]
• Mai 的分数为：b[1] ⊕ b[2] ⊕ ... ⊕ b[n]

若分数不同，分数大的获胜；若分数相同，则为平局。

整体异或不变量

任何一次交换都只是在同一个下标 i 位置交换 a[i] 与 b[i]。
这种操作不会改变 a 与 b 这两个序列中全部元素的集合，因此：

T = a 全体 ⊕ b 全体

在整个游戏过程中保持不变（这是整个 C1/C2 的基础结构）。

同时还成立：

T = Ajisai_score ⊕ Mai_score

这意味着最终的胜负情况只由 T 决定。

• 若 T = 0
  → 两人的最终 XOR 完全相同
  → 游戏必为平局

• 若 T = 1
  → 两人的最终 XOR 不可能相同
  → 必然分出胜负

这一步是 C1 的基础，也是后续 C2 的关键出发点。

接下来进入 C1 的错误思路复盘。

错误解法复盘：误以为“奇偶位置数量”决定胜负

比赛时我最初写出的思路，是基于“统计差异所在的奇数位和偶数位数量”来判断谁能获胜：

• 如果在 奇数位（Ajisai 能操作的位置）出现更多 a[i] != b[i] 的情况
  → Ajisai 更能“影响局势”，认为 Ajisai 会赢

• 如果在 偶数位（Mai 的回合）出现更多差异
  → Mai 会赢

• 如果数量相同，则认为是平局

这是一个看似合理、实际上完全错误的判断。

C1 WA code（我当时的版本）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

#include<bits/stdc++.h>
using namespace std;
int const maxn = 2e5 + 5;

int t, a[maxn], b[maxn];

void op(){
    int n, cnt_odd = 0, cnt_even = 0;
    cin >> n;
    for(int i = 1; i <= n; ++i){
        cin >> a[i];
    }
    for(int i = 1; i <= n; i++){
        cin >> b[i];
        if(a[i] != b[i]){
            if(i & 1){
                cnt_odd++;
            } else{
                cnt_even++;
            }
        }
    }
    if(cnt_odd > cnt_even){
        cout << "Ajisai" << '\n';
    } else if(cnt_odd < cnt_even){
        cout << "Mai" << '\n';
    } else{
        cout << "Tie" << '\n';
    }
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> t;
    while(t--){
        op();
    }
    return 0;
}

错误原因分析

根本问题在于：
XOR 的胜负由唯一的关键下标决定，不由“数量”决定。

在 C1 中，所有元素都是 0/1，若整体异或 T = 1，说明最终两人的分数一高一低，而大小关系由“最后一个能翻转该位的下标”决定。

也就是说：

XOR 的比较不是累计效应，而是“最后一手效果”。

为了更直观地说明问题，我们加入 ASCII 示意图。

示意图（差异位置从后往前扫描）

1
2
3
4
5
6
7

i = 9   a=1 b=1
i = 8   a=0 b=0
i = 7   a=1 b=0   ← 最后一个差异，决定胜负
i = 6   a=0 b=0
i = 5   a=1 b=1
i = 4   a=0 b=0
...

可以看到：

• 下标越靠后，越决定最终的异或结果
• 只要在 i = 7 这里能动手，后面已无下标能覆盖它

因此：

• 若 最后的差异位 是奇数 → Ajisai 操作 → Ajisai 赢 （如示意图所示）
• 若 最后的差异位 是偶数 → Mai 操作 → Mai 赢

无论前面有多少差异位，都被这个 最后的差异位 所覆盖。

为什么统计数量会产生误导？

因为 a[i] != b[i] 是否出现多次完全不重要。
决定 XOR 大小关系的不是次数，而是：

最后一个能改变哪一位的人是谁。

在 C1 中，这个最后位置就是“最后一个差异点”。
由于 XOR 是按位运算，且 C1 只有一位（只有 0/1），因此：

• 若 a[i] != b[i] 在 i = k 处是最后一次出现
• 那么 k 的操作者可以决定自己的最终 XOR 是 1 还是 0

从而直接确定胜负。

错误点总结

1. XOR 的大小不累加，受最后关键位影响
2. C1 只有一个 bit，所以只需找“最后一个差异位置”
3. 差异出现次数完全不影响胜负
4. 正确策略必须基于“顺序博弈 + 最后一手控制权”

接下来进入 C1 的正确解法。

C1 正确解法：最后一个差异下标的操作者获胜

C1 的核心在于：
当整体异或 T = 1 时，最终异或的大小完全由 最后一个能翻转该位的位置 决定。

我们已经在错误分析中看到：
只要知道差异的“最后一个下标”，就能判断胜负。

现在来严格说明这一结构。

1. 当 T = 1 时，胜负由最后一个差异下标决定

在 C1 中，所有元素都是 0 或 1。
最终的分数为：

• Ajisai_score = a[1] ⊕ ... ⊕ a[n]
• Mai_score = b[1] ⊕ ... ⊕ b[n]

因为 T = Ajisai_score ⊕ Mai_score 且 T = 1，
两者的分数必然一为 0、一为 1。

问题变为：

谁能决定某个位置的值在最终 XOR 中是否被计为 1？

XOR 的按位独立性使得“顺序”变得关键

对于序列 a：

最终 a 的 XOR = (((a[1] ⊕ a[2]) ⊕ a[3]) ... ⊕ a[n])

如果我们从左到右分析：

• 一个靠后的元素，其取值变化会覆盖所有更前面元素的影响
• 若前面某个差异位曾试图翻转结果，只要后面存在新的差异位，就可以再次翻转回来

于是结论自然形成：

在 C1 中，最后一个 a[i] != b[i] 的位置，是唯一有决定权的位置。

2. ASCII 示意图

下面是完整示意图（同上，但放在正确解法体系中）：

1
2
3
4
5
6
7
8
9

i = 9   a=1 b=1
i = 8   a=0 b=0
i = 7   a=1 b=0   ← 决胜点（最末一个差异）
i = 6   a=0 b=0
i = 5   a=1 b=1
i = 4   a=0 b=0
i = 3   a=1 b=1
i = 2   a=0 b=0
i = 1   a=1 b=1

• 因为下标 7 是最后一个差异点
• 7 是奇数 → 该回合由 Ajisai 操作
• Ajisai 可以通过“交换 / 不交换”来决定 a[7] 是否变为 1 或 0

从而决定最终自己的 XOR 是否为 1
→ 决定胜负。

若最后的差异下标是偶数，则由 Mai 控制。

3. 正确解法结论化

所以，在 C1 中：

• 扫描从后往前找最后一个 a[i] != b[i] 的下标 i
• 若不存在，则 T = 0 → 平局
• 若存在：
  • i 为奇数 → Ajisai 胜
  • i 为偶数 → Mai 胜

这是 C1 的完整正确解法。

4. C1 AC code

说明：

下方给出的 AC 代码是我在比赛现场写出的实现方式：
逻辑正确，但偏向个人习惯，与本文推导出的理论模型略有差异。
在后续 C2 中，我会给出完全按本文结构写出的“规范解法版本”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<bits/stdc++.h>
using namespace std;
int const maxn = 2e5 + 5;

int t, a[maxn], b[maxn];

void op() {
    int n, cnt_odd = 0, cnt_even = 0, cnt_1 = 0;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        cnt_1 += a[i] ? 1 : 0;
    }
    for (int i = 1; i <= n; ++i) {
        cin >> b[i];
        cnt_1 += b[i] ? 1 : 0;
        if (!(cnt_1 & 1)) {
            cout << "Tie" << '\n';
            return;
        }
        bool last_person; //1->odd 0->even
        for (int i = n; i >= 1; --i) {
            if (a[i] != b[i]) {
                last_person = (i & 1);
                break;
            }
        }
        if (last_person) {
            cout << "Ajisai" << '\n';
        } else {
            cout << "Mai" << '\n';
        }
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> t;
    while (t--) {
        op();
    }
    return 0;
}

C2. Renako Amaori and XOR Game (hard version)

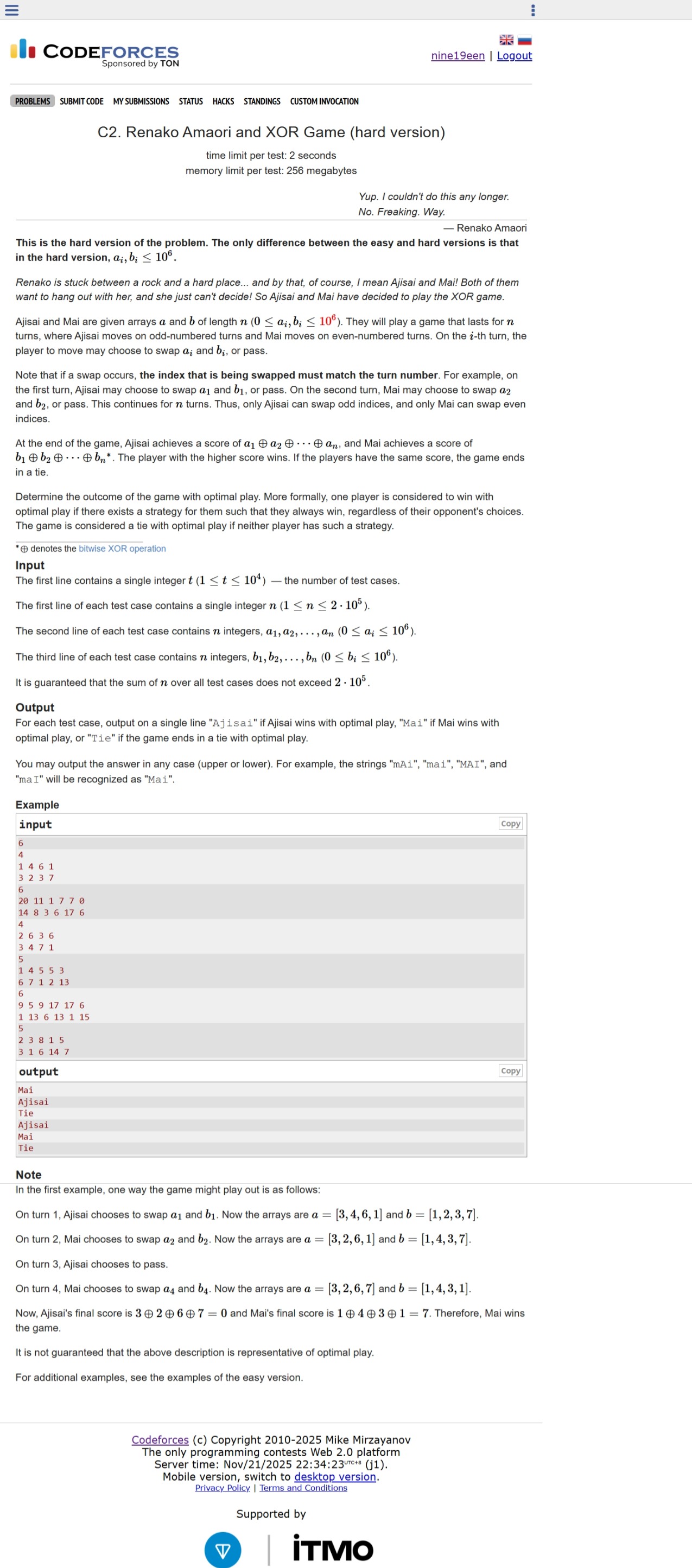
题面

题目翻译

这一题是 C1 的加强版。
给定两个长度为 n 的数组 a 与 b，满足 0 ≤ a[i], b[i] ≤ 10^6。

游戏仍然进行 n 回合：

• 若 i 为奇数，则该回合由 Ajisai 操作；
• 若 i 为偶数，则该回合由 Mai 操作。

在第 i 回合，轮到的玩家可以选择：

• 交换 a[i] 与 b[i]，或者
• 什么也不做（pass）

游戏结束后，得分为：

• Ajisai 的分数：a[1] ⊕ a[2] ⊕ ... ⊕ a[n]
• Mai 的分数：b[1] ⊕ b[2] ⊕ ... ⊕ b[n]

分数更大者获胜，若分数相同则为平局。

与 C1 不同之处在于，这里 a[i] 和 b[i] 不再局限于 0/1，而是可以达到 10^6，也就是包含了更多二进制位，T 不再只可能是 0 或 1，而是一个多 bit 的整数。

整体异或不变量（与 C1 相同的骨架）

和 C1 完全一样，所有操作只在同一位置的 a[i] 与 b[i] 之间做交换，不会引入新数或删除旧数，因此：

T = a 全体 ⊕ b 全体

在整个游戏过程中仍然是一个不变量。

并且依然有：

T = Ajisai_score ⊕ Mai_score

所以：

• 若 T = 0
  → 两人的最终得分完全相同
  → 游戏必为 Tie

• 若 T ≠ 0
  → 两人的最终得分一定不同
  → 必分胜负

到这里为止，C2 与 C1 的结构是同一套骨架：
只要整体异或为 0，游戏就没有悬念，直接平局。
当整体异或不为 0，问题就变成：谁能把最终的数值拉大到对自己有利。

区别在于：C1 中我们只需要处理一个 bit（0/1），而 C2 中要面对的是一个多 bit 整数。

为什么只看最高有效位（msb）

当 T ≠ 0 时，T 是一个多 bit 的整数，例如：

T = 0010 1000 0100₂

这意味着在多个 bit 上，Ajisai 与 Mai 的最终结果存在差异。

但是，对于两个整数的比较，有一个非常重要的事实：

两个整数的大小，只由它们在“最高一个不同的二进制位”上的值决定。

也就是说：

• 找到 Ajisai_score 与 Mai_score 在最高一个不同的 bit
• 在这个 bit 上谁是 1、谁是 0，谁就赢
• 在此之下的所有更低位，统一统统不重要

而由于：

Ajisai_score ⊕ Mai_score = T

那么 T 在某一 bit 上为 1，就说明双方在这一位上必然不同。
特别地，在 T 的最高有效位（记作 msb）上，两人的得分在该位必然一高一低，并且这一位决定最终大小。

用一个 ASCII 示意图表示 T 的 bit 分布（示意）：

1
2
3
4

bit11 bit10 bit9 ... bit3 bit2 bit1 bit0
  1     0    1        0    1    0    0
  ↑
  msb（最高有效位）

在 bit11 这个位置上，T 为 1，代表：

• Ajisai_score 与 Mai_score 在 bit11 这一位上不相同
• 并且 bit11 是它们“从高到低第一个不相同的位”

因此：

• 谁能控制最终在 bit11 上取 1，谁就拥有整个数值比较上的优势
• 低位的翻转（bit10 以下）不会推翻这条结论

换句话说，C2 虽然是多 bit 情况，但在博弈结构上 仍然退化成对 msb 这一位的控制问题：

C2 的本质是：在最高有效位 msb 上进行一场 C1 风格的博弈。

后面的分析要做的，就是精确刻画：
谁拥有对这一位的“最后一次操作权”，也就是谁能在这一位上做出最终决策。

寻找能影响 msb 的最大下标 i_max

我们已经知道：

• 胜负由 T 的最高有效位 msb 决定
• 双方的 XOR 在这一位上必然不同
• 谁能控制最终这一位取值为 1，谁就赢

现在的问题是：

哪些下标 i 能影响 msb 这一位？
谁是最后一个能影响它的人？

关键判定条件

在下标 i，交换与否会造成 msb 这一位的翻转，当且仅当：

((a[i] ⊕ b[i]) >> msb) & 1 == 1

这句话的含义是：

• a[i] ⊕ b[i] 在 msb 位上为 1
• 表示如果交换 a[i] 与 b[i]，那么这一位的贡献会发生改变
• 因此该下标可以真实影响最终比分的最高位

我们称这样的下标为：

“影响 msb 的有效下标”

为什么必须找“最大”的这样的下标？

因为游戏从 1 到 n 顺序进行，越靠后的回合越晚出现。
假设有下面五个可能影响 msb 的下标：

i = 2, 5, 8, 11, 14

真正能决定胜负的只有：

• 最后一个（即 14）
• 因为它会覆盖前面所有的决策效果
• 前面的影响都会被“后继修改”覆盖掉（同 C1）

换句话说：

i_max = 最后一个能影响 msb 的下标
是本题的唯一关键点。

ASCII 示意图（图示 #3）

下面以一个示例说明：

1
2
3
4
5
6

i = 12   (a⊕b 在 msb 位为 1)
i = 11   (a⊕b 在 msb 位为 0)
i = 10   (a⊕b 在 msb 位为 1)
i =  9   (a⊕b 在 msb 位为 1)   ← i_max（最后一个能影响 msb 的位置）
i =  8   (a⊕b 在 msb 位为 0)
...

即使 i = 12 和 i = 10 也能影响 msb 位，
但它们最终都被 i = 9 的操作“覆盖”了：

• 游戏在第 9 回合有最后一次能够改变 msb 的机会
• 之后再没有任何下标能影响 msb
• 所以 i = 9 的操作者可以决定胜负

与 C1 的对应关系

到这里可以看到，C2 的结构与 C1 完全对应：

可以理解为：

• C1 是一个“一维博弈”
• C2 是一个“按 bit 拆开的多维博弈”，但胜负只看最高一维

如何根据 i_max 决定胜负

规则非常简单：

• 若 i_max 为奇数
  → Ajisai 操作
  → Ajisai 可以控制 msb 位置取 1
  → Ajisai 获胜

• 若 i_max 为偶数
  → Mai 操作
  → Mai 可以控制 msb 位置取 1
  → Mai 获胜

这就是 C2 的最终结论。

C2 算法流程与复杂度分析

把前面的分析收束成一个完整的实现流程，大致可以写成如下步骤：

1. 读入 n，以及数组 a、b
2. 计算整体异或 T：
   • T ^= a[i]
   • T ^= b[i]
3. 若 T = 0：
   • 直接输出 Tie，因为此时两人的最终分数必然相等
4. 若 T ≠ 0：
   • 在 0 ~ 20 的 bit 范围内，找到 T 的最高有效位 msb
   • 这一位是唯一决定胜负的关键 bit
5. 从后往前扫下标 i = n ... 1：
   • 判断 (a[i] ⊕ b[i]) 的 msb 位是否为 1
   • 若是，则记录该 i 为 i_max，并停止扫描
6. 根据 i_max 的奇偶性输出胜负：
   • 若 i_max 为奇数 → Ajisai
   • 若 i_max 为偶数 → Mai

复杂度分析

• 计算整体异或 T：O(n)
• 找 msb：bit 扫描，O(log T)，在本题中约为常数（约 20）
• 从后往前找 i_max：O(n)
• 总体时间复杂度：O(n)
• 空间复杂度：O(n)（存下 a、b）

在 n 最多 2 * 10^5 的条件下，这个复杂度完全可以通过所有测试。

C2 AC code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<bits/stdc++.h>
using namespace std;

int t;

void op() {
    int n, xor_sum = 0, msb;
    cin >> n;
    vector<int> a(n + 5), b(n + 5);
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        xor_sum ^= a[i];
    }
    for (int i = 1; i <= n; ++i) {
        cin >> b[i];
        xor_sum ^= b[i];
    }
    if (!xor_sum) {
        cout << "Tie" << '\n';
        return;
    }
    for (int i = 20; i >= 0; --i) {
        if (1 & (xor_sum >> i)) {
            msb = i;
            break;
        }
    }
    for (int i = n; i > 0; --i) {
        if (((a[i] ^ b[i]) >> msb) & 1) {
            cout << ((i & 1) ? "Ajisai" : "Mai") << '\n';
            return;
        }
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> t;
    while (t--) {
        op();
    }
    return 0;
}

XOR 小结与博弈结构回顾（总结）

整篇文章从 C1（0/1 情况）到 C2（多 bit 情况），实际上围绕的是同一个中心主题：

XOR 的结构性 —— 不变量、按位独立性、最高有效位的决定性
以及顺序博弈中“最后一个能改变关键位的人获胜”。

下面将这套结构完整收束，作为本文的最终总结。

1. XOR 的三个核心性质

在这两题中，真正起作用的只有 XOR 的三个基础性质：

• 按位独立性：高位与低位互不影响
• 异或不变量：只交换位置不改变整体 XOR
• 整数大小由最高不同位决定：这保证了 C2 只需处理 msb 一个 bit

其中最关键的，是第三条：
只要最高有效位差异已定，低位就无法影响最终大小。

因此，XOR 博弈的核心往往是：

找到决定关键 bit 的最后一个位置。

2. C1：单 bit 游戏的“最后一手控制权”

在 C1 中：

• 所有元素均为 0 或 1
• 最终 XOR 只有一位
• 胜负完全由最后一个 a[i] != b[i] 的下标决定

这是典型的“顺序博弈 + 最后一手胜”的结构。

3. C2：多 bit 游戏，但仍然只需处理最高 bit

在 C2 中：

• 元素的 bit 数更多
• 整体 XOR T 是一个多 bit 整数
• 但最终大小仍然只由 T 的最高有效位 msb 决定

因此 C2 的实质是：

在 msb 位上跑一遍 C1 的逻辑。

具体表现为：

• 寻找 (a[i] ⊕ b[i]) 在 msb 位上为 1 的最后一个 i
• 该 i 的操作者拥有决定权
• 奇数位 → Ajisai
• 偶数位 → Mai

和 C1 完全平行。

4. 一类 XOR 博弈题的通用做法

通过这两题，我们可以抽象出一类常见 XOR 博弈题的解法框架：

1. 找不变量：整体 XOR 是否为固定？
2. 判断平局条件：如果整体 XOR 为 0，一般直接平局
3. 找关键 bit：通常是 msb
4. 定位关键下标：最后一个能影响关键 bit 的地方
5. 按回合归属输出胜负

许多看似复杂的 XOR 博弈，其实都可以被拆解成这种结构。

5. 本文的意义与后续思考

这篇文章不仅解决了 C1 / C2，也为之后处理此类问题奠定了统一视角：

• 遇到异或类博弈时，先看是否有“不变量”
• 再看是否能按 bit 拆分
• 若能拆分，最高有效位通常是核心
• 判断回合顺序是否决定胜负
• 是否存在“最后一个能翻转关键位的位置”

XOR 本身的逻辑并不复杂，但要真正理解它在博弈中的作用，需要对
“按位独立 + 顺序控制” 有清晰认识。

以上便是本篇的全部内容。

前言

本文复盘洛谷 P1121 环状最大两段子段和 的解题过程。本次复盘的核心算法思路，即 分类讨论 结合 对偶思想，在初版实现中就是正确的。然而，一个由 非空 约束导致的边界情况，使得初版代码无法通过全部测试点。本文将详细分析该边界情况的触发机理，并展示如何通过一行代码进行修复，将80分的实现修正为100分的最终解。

题目分析

提炼题目要素：

1. 布局：环形 排列。a[1] 和 a[n] 相邻。这意味着一个连续子段可以从数组尾部跨越到头部。
2. 目标：选出 两段 不重叠 且 非空 的连续子段，使其和最大。非空 约束是处理边界情况的关键。
3. 约束：N最大为2e5，算法的时间复杂度必须是O(N)或O(N log N)。

此问题需要在环形结构上求解两段子段的和的最大值。重点在于设计一个线性时间复杂度的算法，以处理 环形结构 和 两段选择 的双重约束。

算法设计及实现

V1.0 初版实现 (80分)

设计

在环形结构上直接进行动态规划，因其缺少固定起终点而难以定义状态。因此，采用标准方法，将环形问题分解为线性问题进行处理。

对所有可能的两段子段的选择，按其是否跨越 a[1] 和 a[n] 的连接点，可分为两种情况：

1. 情况一：选择的两段不跨越 a[1]-a[n] 的连接点。
   • 问题转化: 此情况等价于在 链 a[1...n] 上寻找最大两段子段和。
   • 解决方案: 通过枚举分割点来解决。链上的两段最优解 S1 和 S2 之间必定存在一个分割点。
     a. 通过动态规划预处理计算两个辅助数组：
     • max_L_to_R[i]：存储 前缀区间 a[1...i] 内的最大单段子段和。
     • max_R_to_L[i]：存储 后缀区间 a[i...n] 内的最大单段子段和。
       b. 遍历所有可能的分割点 i (1 到 n-1)，计算 max_L_to_R[i] + max_R_to_L[i+1]。
       c. 这些和中的最大值，即为情况一的解。

2. 情况二：选择的两段跨越 a[1]-a[n] 的连接点。
   • 问题转化: 此情况指一段位于数组尾部，另一段位于头部。为简化计算，采用对偶思想。
   • 逻辑原理: (选中元素的和) = (数组总和) - (未选中元素的和)。
   • 核心观察: 若选中的部分是 跨界 的，则未选中的部分必然是 不跨界 的。
   • 再次转化: 最大化 选中元素的和，等价于最小化 未选中元素的和。
   • 解决方案:
     a. 问题转化为：在 链 a[1...n] 上，寻找 最小两段子段和。
     b. 采用与情况一对称的方法，计算 min_L_to_R 和 min_R_to_L 数组，求出链上的最小两段和。
     c. 用 数组总和 减去此值，即为情况二的解。

最终答案为 max(情况一的解, 情况二的解)。该算法的时间复杂度为O(N)。

实现

80分提交记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 2e5 + 5, minn = -1e9;

int n;
ll total_a, a[maxn], max_L_to_R[maxn], dp_max_L_to_R[maxn], max_R_to_L[maxn], dp_max_R_to_L[maxn], min_L_to_R[maxn], dp_min_L_to_R[maxn], min_R_to_L[maxn], dp_min_R_to_L[maxn];

void find_L_to_R() {
    ll max_val = minn, min_val = maxn;
    for (int i = 1; i <= n; ++i) {
        dp_max_L_to_R[i] = max(dp_max_L_to_R[i - 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_L_to_R[i]);
        max_L_to_R[i] = max_val;
        dp_min_L_to_R[i] = min(dp_min_L_to_R[i - 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_L_to_R[i]);
        min_L_to_R[i] = min_val;
    }
}

void find_R_to_L() {
    ll max_val = minn, min_val = maxn;
    for (int i = n; i >= 1; --i) {
        dp_max_R_to_L[i] = max(dp_max_R_to_L[i + 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_R_to_L[i]);
        max_R_to_L[i] = max_val;
        dp_min_R_to_L[i] = min(dp_min_R_to_L[i + 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_R_to_L[i]);
        min_R_to_L[i] = min_val;
    }
}

ll case_1() {
    ll max_val = minn;
    for (int i = 1; i < n; ++i) {
        max_val = max(max_val, max_L_to_R[i] + max_R_to_L[i + 1]);
    }
    return max_val;
}

ll case_2() {
    ll min_val = maxn;
    for (int i = 1; i < n; ++i) {
        min_val = min(min_val, min_L_to_R[i] + min_R_to_L[i + 1]);
    }
    return total_a - min_val;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        total_a += a[i];
    }
    find_L_to_R();
    find_R_to_L();
    cout << max(case_1(), case_2());
    return 0;
}

错误分析

• 问题根源：
  算法的理论模型正确，但代码实现未处理一个由 非空 约束引发的特殊情况。该问题在输入数组 全为负数 的测试点上触发。

• 错误原因：

  1. 当数组全为负数时，为使和最小，算法会选择尽可能多的元素。因此，计算出的 链上最小两段和 等于 数组总和。
  2. 此时，case_2() 函数的计算 total_a - min_val 变为 total_a - total_a，结果为 0。
  3. 根据 非空 约束，对于全负数组，任意两段非空子段的和必须为负数。case_1() 会正确计算出这个负数的最优解。
  4. 最终，main 函数在 max(一个正确的负数, 0) 的比较中，会错误地选择 0。
  5. 这个结果 0 对应于 未选中全部元素 的情况，即 选中了空集，这与题目的 非空 约束相悖。

V2.0 修正实现 (AC)

设计

问题已明确：当 链上最小两段和 == 数组总和 时，case_2() 会产生一个违反约束的无效解 0。

修正的目标是：识别此情况，并确保该无效解不被选为最终答案。

• 解决方案: 修改 case_2() 函数的返回值。当 total_a == min_val 的条件成立时，函数不返回 0，而是返回一个理论上的极小值 LLONG_MIN。
• 效果: 任何合法的解（即使是负数）都必然大于 LLONG_MIN。因此，在最终的 max 比较中，case_1() 计算出的合法解会自动取代 case_2() 返回的 LLONG_MIN，从而保证结果的正确性。

实现

AC提交记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 2e5 + 5;

int n;
ll total_a, a[maxn], max_L_to_R[maxn], dp_max_L_to_R[maxn], max_R_to_L[maxn], dp_max_R_to_L[maxn], min_L_to_R[maxn], dp_min_L_to_R[maxn], min_R_to_L[maxn], dp_min_R_to_L[maxn];

void find_L_to_R() {
    ll max_val = LLONG_MIN, min_val = LLONG_MAX;
    for (int i = 1; i <= n; ++i) {
        dp_max_L_to_R[i] = max(dp_max_L_to_R[i - 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_L_to_R[i]);
        max_L_to_R[i] = max_val;
        dp_min_L_to_R[i] = min(dp_min_L_to_R[i - 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_L_to_R[i]);
        min_L_to_R[i] = min_val;
    }
}

void find_R_to_L() {
    ll max_val = LLONG_MIN, min_val = LLONG_MAX;
    for (int i = n; i >= 1; --i) {
        dp_max_R_to_L[i] = max(dp_max_R_to_L[i + 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_R_to_L[i]);
        max_R_to_L[i] = max_val;
        dp_min_R_to_L[i] = min(dp_min_R_to_L[i + 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_R_to_L[i]);
        min_R_to_L[i] = min_val;
    }
}

ll case_1() {
    ll max_val = LLONG_MIN;
    for (int i = 1; i < n; ++i) {
        max_val = max(max_val, max_L_to_R[i] + max_R_to_L[i + 1]);
    }
    return max_val;
}

ll case_2() {
    ll min_val = LLONG_MAX;
    for (int i = 1; i < n; ++i) {
        min_val = min(min_val, min_L_to_R[i] + min_R_to_L[i + 1]);
    }
    return total_a == min_val ? LLONG_MIN : total_a - min_val;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        total_a += a[i];
    }
    find_L_to_R();
    find_R_to_L();
    cout << max(case_1(), case_2());
    return 0;
}

• 实现细节剖析
  核心改动位于 case_2() 函数的返回语句：
  return total_a == min_val ? LLONG_MIN : total_a - min_val;
  该行代码使用三元运算符，将对特殊情况的判断和处理封装在函数内部，解决了问题。

• 健壮性提升
  AC代码将所有用于初始化的极大/极小值，从硬编码的数值（如1e9）替换为标准库 <climits> 中定义的 LLONG_MAX 和 LLONG_MIN。这使代码不依赖于对题目数据范围的假设，提高了通用性和健壮性。

P.S. 完整手稿

总结

1. 环形问题处理方法：分类讨论 结合 对偶思想 是处理此类环形数组问题的有效方法，可将问题转化为线性空间下的计算。
2. 边界情况的重要性：必须分析 全正、全负 等特殊数据集。题目的 非空 等约束，在这些边界情况下是决定算法正确性的关键。
3. 一种处理无效解的技巧：当算法的一个分支可能产生逻辑上无效的解时，可以使其返回一个在最终聚合操作（如max或min）中必定会被淘汰的值（如LLONG_MIN或LLONG_MAX），从而避免复杂的外部逻辑判断。

前言

最近，我解决了一道经典的 环形DP 问题。该问题具有较强的迷惑性，我设计了一个看似正确的线性DP模型，实际上忽略了问题最核心的 环形 约束。本文旨在完整复盘从一个70分的线性解，到一个90分的 错误补丁 解，最终到100分AC的 破环成链 正解的全过程，深入剖析每一步的思维误区与正确建模的关键。

题目分析

P1133 教主的花园

提炼题目要素：

1. 布局：环形 排列。
2. 约束：任何一棵树必须比其左右相邻的树 同时更高或更矮，形成 波峰 或 波谷。
3. 目标：观赏价值总和最大。

这是一个动态规划问题。核心在于状态的设计。为了存储输入的观赏价值，我使用了一个 Plant_Position 结构体，其中 pos[i].ten, pos[i].twenty, pos[i].thirty 持有位置 i 的相应价值。

为了判断位置 i 的种植是否合法，不仅需要知道位置 i-1 的高度，还需要知道 i-1 相对于 i-2 的趋势，这样才能决定 i 的合法走向。因此，一个三维状态是必要的：dp[i][j][k]。

• i：表示正在考虑第 i 棵树。
• j：表示第 i 棵树的高度。我们用 1, 2, 3 分别代表高度 10, 20, 30。
• k：表示第 i 棵树的形态。
  • k=0：第 i 棵树是 波谷，即 H[i-1] > H[i]，从 i-1 到 i 是 下降 趋势。
  • k=1：第 i 棵树是 波峰，即 H[i-1] < H[i]，从 i-1 到 i 是 上升 趋势。

dp[i][j][k] 的值，就代表满足以上定义时的最大观赏价值。

算法设计及实现

V1.0 线性DP的初步尝试 (70分)

设计

最初的方案完全忽略了 环形 约束，将花园视为一个从 1 到 n 的 线性序列。基于上述 dp[i][j][k] 状态，可以推导出所有合法的状态转移方程。

状态转移方程详解：

1. 目标状态: dp[i][1][0] (高度 10 , 波谷/下降)

   • 逻辑: 要下降到高度 10 ，前一个位置 i-1 的高度必须是 20 或 30 。同时，为了形成波谷，前一个位置 i-1 必须是波峰（上升趋势，k=1）。
   • 方程: dp[i][1][0] = max(dp[i-1][2][1], dp[i-1][3][1]) + pos[i].ten

2. 目标状态: dp[i][2][0] (高度 20 , 波谷/下降)

   • 逻辑: 要下降到高度 20 ，前一个位置 i-1 的高度必须是 30 。前一个位置 i-1 必须是波峰（上升趋势，k=1）。
   • 方程: dp[i][2][0] = dp[i-1][3][1] + pos[i].twenty

3. 目标状态: dp[i][2][1] (高度 20 , 波峰/上升)

   • 逻辑: 要上升到高度 20 ，前一个位置 i-1 的高度必须是 10 。前一个位置 i-1 必须是波谷（下降趋势，k=0）。
   • 方程: dp[i][2][1] = dp[i-1][1][0] + pos[i].twenty

4. 目标状态: dp[i][3][1] (高度 30 , 波峰/上升)

   • 逻辑: 要上升到高度 30 ，前一个位置 i-1 的高度可以是 10 或 20 。前一个位置 i-1 必须是波谷（下降趋势，k=0）。
   • 方程: dp[i][3][1] = max(dp[i-1][1][0], dp[i-1][2][0]) + pos[i].thirty

不可达状态:

• dp[i][1][1] (上升到最低点) 和 dp[i][3][0] (下降到最高点) 是不可能出现的。这些状态的值应保持为极小值，不参与计算。

实现

该方案的实现直接从 i=1 循环到 n，并在最后取 dp[n] 所有合法状态的最大值作为结果。

70分提交记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][8][7];
Plant_Position pos[maxn];

void dp_10_0(int idx) {
    dp[idx][1][0] = max(dp[idx - 1][2][1], dp[idx - 1][3][1]) + pos[idx].ten;
}

void dp_20_0(int idx) {
    dp[idx][2][0] = dp[idx - 1][3][1] + pos[idx].twenty;
}

void dp_20_1(int idx) {
    dp[idx][2][1] = dp[idx - 1][1][0] + pos[idx].twenty;
}

void dp_30_1(int idx) {
    dp[idx][3][1] = max(dp[idx - 1][1][0], dp[idx - 1][2][0]) + pos[idx].thirty;
}

ll DP() {
    for (int i = 1; i <= n; i++) {
        dp_10_0(i);
        dp_20_0(i);
        dp_20_1(i);
        dp_30_1(i);
    }
    return max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    cout << DP();
    return 0;
}

错误分析

• 问题根源：
  该方案计算出的结果是 线性排列 下的最优解。但题目要求的是 环形排列。线性最优解的第 n 个位置和第 1 个位置的状态，很可能不满足高低交错的约束，因此该解对于环形问题是 非法的。

V2.0 “打补丁”的错误修正 (90分)

设计

在提交V1.0后，我意识到了环形约束的问题。此时产生了一个错误的修正思路：先算出线性最优，再检查它是否满足环形约束。

这个思路最初的实现是一个复杂且繁琐的 while 循环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

ans.push_back(dp[n][1][0]);
ans.push_back(dp[n][2][0]);
ans.push_back(dp[n][2][1]);
ans.push_back(dp[n][3][1]);
sort(ans.begin(), ans.end());
bool y[5] = {0};
while (1) {
    if (ans.back() == dp[n][2][0] && !y[0]) {
        if (pos[1].twenty < pos[1].thirty) {
            cout << ans.back();
            return;
        }
        else {
            y[0] = true;
            ans.pop_back();
            continue;
        }
    }
    if (ans.back() == dp[n][2][1] && !y[1]) {
        if (pos[1].twenty < pos[1].ten) {
            cout << ans.back();
            return;
        }
        else {
            y[1] = true;
            ans.pop_back();
            continue;
        }
    }
    cout << ans.back();
    return;
}

这个复杂的 while 最终被我精简为两个 if 语句：

1
2
3
4
5
6
7

if (pos[1].twenty > pos[1].ten) {
    dp[n][2][1] = 0;
}
if (pos[1].twenty > pos[1].thirty) {
    dp[n][2][0] = 0;
}
cout << max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));

if 虽比 while 精简了很多，其内在的错误逻辑是相同的。这个 “补丁” 的意图是，从线性DP算出的几个最优候选解中，通过一套逻辑来 推断 并 验证 起点是否合法。

其验证逻辑如下：

1. 无约束情况：如果线性最优解的终点是 dp[n][1][0] ( H=10 , 下降) 或 dp[n][3][1] ( H=30 , 上升)，则直接接受。

   • 推断: 如果 H[n]=10，则环要求 H[1] > 10，即 H[1] 可以是 20 或 30 。因为有两个选择，代码便假设总能找到一个合法的起点，无需干预。H[n]=30 同理。

2. 约束情况 1: 当考虑终点为 dp[n][2][1] ( H=20 , 上升) 的路径时。

   • 推断: 这个终点状态意味着 H[n-1]=10。为了构成环，H[1] 必须小于 H[n]=20，所以 H[1] 必须是 10。
   • 验证: 此时，代码进行一次 贪心 检查：if (pos[1].twenty > pos[1].ten)。这个判断的逻辑是：“如果在起点上，种 20 的观赏价值比种 10 要高，那么一个真正最优的路径，当初在起点时就 不可能 选择种 10 ”。基于这个贪心假设，如果条件成立，就认为这条要求起点为 10 的路径不可能是最优解，于是通过 dp[n][2][1] = 0 将其作废。

3. 约束情况 2: 当考虑终点为 dp[n][2][0] ( H=20 , 下降) 的路径时。

   • 推断: 这个终点状态意味着 H[n-1]=30。为了构成环，H[1] 必须大于 H[n]=20，所以 H[1] 必须是 30。
   • 验证: 类似地，代码进行贪心检查 if (pos[1].twenty > pos[1].thirty)。如果种 20 的价值更高，就认为这条要求起点为 30 的路径不可能是最优解，将其作废。

实现

90分提交记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][8][7];
Plant_Position pos[maxn];
vector<ll> ans;

void dp_10_0(int idx) {
    dp[idx][1][0] = max(dp[idx - 1][2][1], dp[idx - 1][3][1]) + pos[idx].ten;
}

void dp_20_0(int idx) {
    dp[idx][2][0] = dp[idx - 1][3][1] + pos[idx].twenty;
}

void dp_20_1(int idx) {
    dp[idx][2][1] = dp[idx - 1][1][0] + pos[idx].twenty;
}

void dp_30_1(int idx) {
    dp[idx][3][1] = max(dp[idx - 1][1][0], dp[idx - 1][2][0]) + pos[idx].thirty;
}

void DP() {
    for (int i = 1; i <= n; i++) {
        dp_10_0(i);
        dp_20_0(i);
        dp_20_1(i);
        dp_30_1(i);
    }
    if (pos[1].twenty > pos[1].ten) {
        dp[n][2][1] = 0;
    }
    if (pos[1].twenty > pos[1].thirty) {
        dp[n][2][0] = 0;
    }
    cout << max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    DP();
    return 0;
}

错误分析

• 根本性缺陷：
  此方案的失败，并非因为 if 语句这个 补丁 本身不够精巧。恰恰相反，它很好地浓缩了前一版 while 循环的意图，是一个逻辑上很优质的补丁。

  真正的错误出在算法的 根本设计 上。这种 事后补救 的方法，就相当于把一条通往错误方向的道路修得非常漂亮，但道路再好，也无法到达正确的终点。

  其核心谬误在于，它错误地假设了 环形最优解一定包含在线性最优解之中。而事实上，真正的环形最优解，其线性部分可能根本不是最优的。代码只检查了少数几个 线性最优 的候选者，而真正的答案可能在第一次DP时，就因为在线性排列上得分不够高而被直接淘汰，永远没有机会被最后的 if 语句检查。这是一种典型的 局部最优陷阱。

V3.0 “破环成链”的正确解法 (AC)

设计

正确的做法是放弃 事后补救，采用处理环形问题的 标准范式——破环成链。

其核心思想是，将一个复杂的环形问题，分解为几个独立的、带有明确起始和结束约束 的线性问题。

具体方案是，通过一个外层循环，强制指定 第 1 棵树 的高度（分三种情况： H=10 , H=20 , H=30 ）。对每种情况独立进行一次从2到n的线性DP，并在最后根据固定的起点，对终点 dp[n] 的状态进行合法性筛选。

可行性分析

• 时间复杂度: 每次DP的计算量是 O(n)。总共进行3次独立的DP，所以总时间复杂度依然是 O(n)。
• 空间复杂度: O(n)。
• 结论: 方案高效可行。

实现

AC提交记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][5][5], ans;
Plant_Position pos[maxn];

void DP() {
    ll ans = 0;
    for (int i = 1; i <= 3; i++) {
        if (i == 1) {
            dp[1][1][0] = pos[1].ten;
        }
        else if (i == 2) {
            dp[1][2][0] = pos[1].twenty, dp[1][2][1] = pos[1].twenty;
        }
        else if (i == 3) {
            dp[1][3][1] = pos[1].thirty;
        }
        for (int i = 2; i <= n; i++) {
            dp[i][1][0] = max(dp[i - 1][2][1], dp[i - 1][3][1]) + pos[i].ten;
            dp[i][2][0] = dp[i - 1][3][1] + pos[i].twenty;
            dp[i][2][1] = dp[i - 1][1][0] + pos[i].twenty;
            dp[i][3][1] = max(dp[i - 1][1][0], dp[i - 1][2][0]) + pos[i].thirty;
        }
        if (i == 1) {
            ans = max(ans, max(dp[n][2][1], dp[n][3][1]));
        }
        else if (i == 2) {
            ans = max(ans, max(dp[n][1][0], dp[n][3][1]));
        }
        else if (i == 3) {
            ans = max(ans, max(dp[n][1][0], dp[n][2][0]));
        }
        memset(dp, 0, sizeof(dp));
    }
    cout << ans;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    DP();
    return 0;
}

• 实现细节剖析
  该方案的精髓在于，将环形约束从一个 事后检查 的难题，转化为了一个 顶层设计 的分类讨论。在固定了起点后，最后结算时对终点的筛选逻辑如下：

  1. 若起点 H[1]=10 (波谷):

     • 为构成环，终点 H[n] 必须是波峰，且 H[n] > H[1]。
     • 合法终点状态：dp[n][2][1] ( H=20 , 上升) 和 dp[n][3][1] ( H=30 , 上升)。
     • 候选答案: max(dp[n][2][1], dp[n][3][1])

  2. 若起点 H[1]=20 (波峰或波谷):

     • 为构成环，若 H[n] 是波峰，则 H[n] > H[1]；若 H[n] 是波谷，则 H[n] < H[1]。
     • 合法终点状态：dp[n][3][1] ( H=30 , 上升) 和 dp[n][1][0] ( H=10 , 下降)。
     • 候选答案: max(dp[n][3][1], dp[n][1][0])

  3. 若起点 H[1]=30 (波峰):

     • 为构成环，终点 H[n] 必须是波谷，且 H[n] < H[1]。
     • 合法终点状态：dp[n][1][0] ( H=10 , 下降) 和 dp[n][2][0] ( H=20 , 下降)。
     • 候选答案: max(dp[n][1][0], dp[n][2][0])

  最终答案就是这三个候选答案中的最大值。这种精确的筛选保证了最终解的合法性。

总结

1. 问题建模是关键：正确识别并处理 环形 这一核心模型，是解决本题的钥匙。直接套用线性模型会导致从根本上偏离题意。
2. 警惕“打补丁”式的修正：当发现算法有漏洞时，复杂的 事后检查 逻辑往往是错误或不完备的。正确的做法是回到设计的起点，思考如何将约束从一开始就融入算法模型。
3. 掌握标准范式：破环成链 是解决几乎所有环形DP、环形数组问题的通用且强大的思想，必须熟练掌握。

前言

本题同样由那位BUAA大佬分享。

不久前，我用树状数组解决了洛谷上的逆序对模板题 。因此，当我初见这道 逆序 k 倍对 时，第一反应便是：这一定是模板的变体，核心工具依然是那个熟悉的树状数组。然而，从模板代码到这道题的AC，并非简单的复制粘贴，而是一段充满思考的魔改之旅。本文旨在完整复盘，我是如何基于逆序对模板的思路，一步步识别问题差异、调整关键逻辑，最终将一份模板代码成功改造为本题的解答。

题目

题目描述

给定一个序列 a₁, a₂, …, aₙ 和一个正整数 k，如果 1 ≤ i < j ≤ n 且 aᵢ > k · aⱼ，我们就将 (i, j) 称作一个逆序 k 倍对。请你计算序列中逆序 k 倍对的个数。

输入格式

第一行两个正整数 n, k (1 ≤ n ≤ 10⁵, 1 ≤ k ≤ 10)。
第二行 n 个正整数 a₁, a₂, …, aₙ (1 ≤ aᵢ < 2³¹)。
为了提高区分度，对于得分占比 10% 的测试点，我们保证 1 ≤ n ≤ 100。

输出格式

一行一个非负整数，表示序列中逆序 k 倍对的个数。

输入样例

1
2

5 2
5 4 3 2 1

输出样例

1

4

题目分析

首先肯定要从那道经典的逆序对模板题开始分析。它的问题是统计 i < j 且 a[i] > a[j] 的数对。我当时AC的思路是：

• 从左到右遍历数组，对于每个数 a[j]。
• 利用树状数组，查询在它之前已经出现过的数中，有多少个大于 a[j]。
• 将这些查询结果累加，就是答案。
• 查询结束后，再将 a[j] 本身的信息更新到树状数组中。

当时的AC代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n;
vector<int>a, b;

int Lowbit(int x){
	return x & -x;
}

ll Sum(int x, ll arr[]){
	ll ansSUM = 0;
	for(int i = x; i != 0; i -= Lowbit(i)){
		ansSUM += arr[i];
	}
	return ansSUM;
}

void Update(int x, int add, int size, ll arr[]){
	for(int i = x; i <= size; i += Lowbit(i)){
		arr[i] += add;
	}
	return;
}

int main(){
	cin >> n;
	a.reserve(n + 5);
	b.reserve(n + 5);
	for(int i = 1; i <= n; i++){
		int num;
		cin >> num;
		a.push_back(num);
		b.push_back(num);
	}
	sort(b.begin(), b.end());
	b.erase(unique(b.begin(), b.end()), b.end());
	int size = b.size();
	ll c[size + 5] = {0}, ans[size + 5] = {0};
	int cnt = 0;
	for(int p : a){
		cnt++;
		int idx = lower_bound(b.begin(), b.end(), p) - b.begin() + 1;
		Update(idx, 1, size, c);
		Update(idx, cnt - Sum(idx, c), size, ans);
	}
	cout << Sum(size, ans);
	return 0;
}

这个框架非常清晰。现在，面对k倍逆序对，唯一的不同点，就是判断条件从 a[i] > a[j] 变成了 a[i] > k * a[j]。

这意味着，我的改造也必须围绕这个变化点展开。当我遍历到 a[j] 时，我需要查询的不再是比 a[j] 大的数，而是比 k * a[j] 大的数。

这个看似微小的变化，却直接影响了算法的基石——离散化。在原模板中，我们只需要对数组 a 中的值进行离散化。但现在，为了能查询 k * a[j] 的相关信息，我们必须将所有可能作为查询边界的 k * a[j] 也一并纳入离散化的范围。

这就是从模板到AC的关键一步：识别出查询目标的变化，并相应地扩大离散化的集合。

算法设计及实现

我的整个解题过程，可以看作是对逆序对模板代码的一次定向升级。

核心思路：模板的演进

1. 继承模板框架：

   • 整体的算法流程完全继承自逆序对模板：遍历数组 -> 查询贡献 -> 更新数据 -> 累加结果。
   • 核心数据结构依然锁定为树状数组，因为它能高效地完成我们需要的单点更新和前缀和查询。
   • 由于 a[i] 的值域依然很大，离散化这一前置步骤也必须保留。

2. 定位改造核心：查询目标的变化

   • 模板的查询逻辑是：贡献 = 总数 - 小于等于a[j]的个数。
   • 本题的查询逻辑变为：贡献 = 总数 - 小于等于k*a[j]的个数。
   • 这个k*a[j]就是本次改造需要处理的新元素。

3. 升级离散化：

   • 模板：离散化集合仅包含 { a[1], a[2], ..., a[n] }。
   • 本题：离散化集合必须扩大，同时包含 { a[1], ..., a[n] } 和 { k*a[1], ..., k*a[n] }。因为树状数组的下标是基于离散化后的排名，我们既需要能更新 a[j] 对应的排名，也需要能查询 k*a[j] 对应的排名。将它们全部放入一个集合中进行离散化，才能建立统一的“度量衡”。

4. 微调主逻辑

   • 在主循环中，对于当前元素 p (即a[j])：
     • 首先，找到 p 离散化后的排名 idx。
     • 然后，找到 k*p 离散化后的排名 idx2。
     • 计算贡献值：ans += cnt - Sum(idx2, c)。这里的 cnt 是已处理元素个数，Sum(idx2, c) 则是利用树状数组查到的、前面出现过且值小于等于 k*p 的元素个数。
     • 最后，执行和模板完全一样的更新操作：Update(idx, 1, size, c)，将 p 的出现次数记录到树状数组中。

可行性分析

这次“魔改”并没有改变算法的根本结构。

• 时间复杂度:

  • 离散化集合的大小最多变为 2n。排序的复杂度依然是 O(n log n)。
  • 主循环中，树状数组和 lower_bound 的操作复杂度仍为 O(log n)。
  • 总时间复杂度保持在 O(n log n)，完全可以通过。

• 空间复杂度:

  • 辅助数组 b 和树状数组 c 的大小变为原来的两倍左右，空间复杂度依然是 O(n)。

• 结论：
  通过精准地定位差异并对离散化这一关键步骤进行升级，我们成功地将逆序对模板适配到了新问题上，方案高效可行。

实现

最终的AC代码，清晰地保留了逆序对模板的骨架，但在离散化的部分，能明显看到为了适应新规则而做的扩展。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n, k;
ll ans;
vector<int>a, b;

int Lowbit(int x){
	return x & -x;
}

ll Sum(int x, ll arr[]){
	ll ansSUM = 0;
	for(int i = x; i != 0; i -= Lowbit(i)){
		ansSUM += arr[i];
	}
	return ansSUM;
}

void Update(int x, int add, int size, ll arr[]){
	for(int i = x; i <= size; i += Lowbit(i)){
		arr[i] += add;
	}
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cin >> n >> k;
	a.reserve(n + 5);
	b.reserve(2 * n + 5);
	for(int i = 1; i <= n; i++){
		int num;
		cin >> num;
		a.push_back(num);
		b.push_back(num);
		b.push_back(k * num);
	}
	sort(b.begin(), b.end());
	b.erase(unique(b.begin(), b.end()), b.end());
	int size = b.size();
	ll c[size + 5] = {0};
	ll cnt = 0;
	for(int p : a){
		cnt++;
		int idx = lower_bound(b.begin(), b.end(), p) - b.begin() + 1;
		int idx2 = lower_bound(b.begin(), b.end(), p * k) - b.begin() + 1;
		Update(idx, 1, size, c);
		ans += cnt - Sum(idx2, c);
	}
	cout << ans;
	return 0;
}

代码对比

整个改造过程实际只涉及两个关键环节。

1. 扩展离散化集合

模板代码：仅收集原数组中的值。

1
2
3
4
5
6
7

// 离散化集合 b 只需包含 a 内的值
for(int i = 1; i <= n; i++){
    int num;
    cin >> num;
    a.push_back(num);
    b.push_back(num);
}

本题代码：同时收集原数值与其 k 倍值。

1
2
3
4
5
6
7
8

// 离散化集合 b 必须同时包含 a 内的值及其 k 倍
for(int i = 1; i <= n; i++){
    ll num;
    cin >> num;
    a.push_back(num);
    b.push_back(num);
    b.push_back(k * num); // 【改动】为查询 k*p 预作准备
}

原因：树状数组需要查询 k*p 的排名，因此必须在一开始就将所有可能的 k*p 值纳入离散化，以建立统一的排名体系。

2. 变更查询边界

模板代码：查询大于 p 的元素个数。

1
2
3
4
5
6
7
8
9
10

for(int p : a){
    // 查询和更新都使用 p 自身的排名
    int idx = lower_bound(b.begin(), b.end(), p) - b.begin() + 1;
    
    // 查询边界是 p 本身
    ans += cnt - Sum(idx, c);
    
    Update(idx, 1, size, c);
    cnt++;
}

本题代码：查询大于 k*p 的元素个数。

1
2
3
4
5
6
7
8
9
10
11
12

for(ll p : a){
    // 更新时用 p 的排名
    int idx = lower_bound(b.begin(), b.end(), p) - b.begin() + 1;
    // 【改动】计算新的查询边界 k*p 的排名
    int idx2 = lower_bound(b.begin(), b.end(), p * k) - b.begin() + 1;
    
    // 【改动】使用新的排名 idx2 进行查询
    ans += cnt - Sum(idx2, c);
    
    Update(idx, 1, size, c);
    cnt++;
}

原因：题目的核心条件从 > p 变为 > k*p，因此计算贡献时，传入 Sum 函数的参数，必须是 k*p 对应的排名，而非 p 的排名。

P.S. 例行在最后放上做题手稿

总结

1. 模型识别与套用：将新问题关联到已知的算法模型（本题的逆序对模板），以此为基础快速构建解题框架。
2. 分析核心差异：精准定位问题变体的关键不同点。本题的核心差异在于判断条件从 a[i] > a[j] 变更为 a[i] > k * a[j]。
3. 模块化调整：根据核心差异，修改算法中受影响的模块。此题中，查询条件的变更，直接决定了离散化的数据集合必须相应地扩展。
4. 理解功能而非形式：掌握算法中每个模块的功能目的是解决问题的关键。这使得我们能根据问题变化，对模板进行有效调整，而不是进行无效的生搬硬套。

前言

本题由某位BUAA大佬分享。

初见这道图形题时，我被其酷似分形的演变过程所吸引。它看似是一个纯粹的图形模拟题，但随着操作次数 n 的增加，图形的尺寸和复杂性都呈爆炸式增长，让我意识到简单的暴力绘制绝非正解。本文旨在复盘我如何从繁杂的图形变化中发现并实现一个精妙的递推关系，最终优雅地解决这个问题的全过程。

题目

背景

丁香花通常由四片花瓣组成，四片花瓣的位置关系可以简要用图1表示。

单单四个正方形显然还不能表达丁香花的魅力，因此我们将该图形进行一次操作，包含以下两个步骤：

1. 将图形重复4次，如图2所示；
2. 将图形旋转45度，如图3所示。

我们将上述两个步骤整体称为一次操作。在图3基础上再重复一次操作，我们就能得到图4。

图1: 基础图形	图2: 基础图形重复四次	图3: 进行一次操作后	图4: 进行两次操作后

描述

本题需要你编程绘出进行了 n 次操作后的图形（注意：基础图形为进行了 0 次操作的图形）。

输出时，图形中有正方形的位置输出一个字符 o，没有正方形的位置输出一个空格 。行末的空格可以忽略。

例如，对于图1 (n=0)，应该输出为：

1
2
3

  o
o   o
  o

又如，对于图4 (n=2)，应该输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

            o     o
          o   o o   o
            o     o
            o     o
          o   o o   o
  o     o   o     o   o     o
o   o o   o         o   o o   o
  o     o             o     o
  o     o             o     o
o   o o   o         o   o o   o
  o     o   o     o   o     o
          o   o o   o
            o     o
            o     o
          o   o o   o
            o     o

输入

输入一个非负整数 n，表示操作的次数。

数据保证 0 <= n <= 6。

输出

输出经过 n 次操作后对应的图形。

特别注意：为了方便在控制台进行输出，当操作次数 n 为奇数时，请将图形旋转45度再输出。

输入样例

1

1

输出样例

1
2
3
4
5
6

  o     o
o   o o   o
  o     o
  o     o
o   o o   o
  o     o