丁香花分形·复盘——从递推关系中洞悉分形之美

Posted on In

前言

本题由某位BUAA大佬分享。

初见这道图形题时，我被其酷似分形的演变过程所吸引。它看似是一个纯粹的图形模拟题，但随着操作次数 n 的增加，图形的尺寸和复杂性都呈爆炸式增长，让我意识到简单的暴力绘制绝非正解。本文旨在复盘我如何从繁杂的图形变化中发现并实现一个精妙的递推关系，最终优雅地解决这个问题的全过程。

题目

背景

丁香花通常由四片花瓣组成，四片花瓣的位置关系可以简要用图1表示。

单单四个正方形显然还不能表达丁香花的魅力，因此我们将该图形进行一次操作，包含以下两个步骤：

  1. 将图形重复4次，如图2所示；
  2. 将图形旋转45度，如图3所示。

我们将上述两个步骤整体称为一次操作。在图3基础上再重复一次操作，我们就能得到图4。
图1: 基础图形 图2: 基础图形重复四次 图3: 进行一次操作后 图4: 进行两次操作后

描述

本题需要你编程绘出进行了 n 次操作后的图形（注意：基础图形为进行了 0 次操作的图形）。

输出时，图形中有正方形的位置输出一个字符 o，没有正方形的位置输出一个空格 。行末的空格可以忽略。

例如，对于图1 (n=0)，应该输出为：

1
2
3
  o
o   o
  o

又如，对于图4 (n=2)，应该输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
            o     o
          o   o o   o
            o     o
            o     o
          o   o o   o
  o     o   o     o   o     o
o   o o   o         o   o o   o
  o     o             o     o
  o     o             o     o
o   o o   o         o   o o   o
  o     o   o     o   o     o
          o   o o   o
            o     o
            o     o
          o   o o   o
            o     o

输入

输入一个非负整数 n，表示操作的次数。

数据保证 0 <= n <= 6。

输出

输出经过 n 次操作后对应的图形。

特别注意：为了方便在控制台进行输出，当操作次数 n 为奇数时，请将图形旋转45度再输出。

输入样例

1
1

输出样例

1
2
3
4
5
6
  o     o
o   o o   o
  o     o
  o     o
o   o o   o
  o     o

题目分析

理解题目后，我们可以将一次操作分解为两个基本步骤的组合：

  1. 膨胀：将当前图形作为单元，无重叠地平铺成一个 2x2 的更大图形。
  2. 重组：将膨胀后得到的四个象限进行有重叠的重新排列，形成类似旋转45度的视觉效果。

直接模拟这个过程的难点在于第二步（重组）。每次重组后，新图形的边长是多少？四个象限应该放置在哪个精确的坐标上？这些参数的变化并非线性，如果不能找到其规律，算法将无从下手。因此，整个问题的核心，从如何画图转变成了如何计算每一步操作的画布尺寸与布局坐标。

我的解法选择了一个迭代的思路，从 n=0 的基础图形出发，循环 n 次，每次迭代生成下一阶段的图形。这个迭代过程并非一成不变，而是根据迭代次数的奇偶，执行两种截然不同的生成逻辑。

算法设计及实现

我的算法将题目中抽象的“一次操作”，具象化为一次奇数步膨胀和一次偶数步重组的交替执行。通过一个 for 循环，我们模拟 n 次这样的交替演变，最终得到目标图形。

核心思路：奇偶交替的迭代生成

我们用一个 for 循环从 i=1 到 n 进行迭代，其中 i 代表当前是第几次演变。

  1. 当 i 为奇数时：膨胀阶段

    • 任务：执行纯粹的复制与放大。
    • 实现：我们将上一步（i-1）得到的完整图形（记为 temp）视为一个“瓦片”。然后，在一个尺寸为 a_temp * 2 的新画布（记为 pic）上，将这个瓦片无重叠地铺满 pic 的四个象限。这一步非常直观，图形的结构不变，只是尺寸翻倍。

  2. 当 i 为偶数时：重组阶段

    • 任务：执行复杂的重叠与收缩。
    • 实现：这一步处理的是奇数阶段生成的、由四个象限组成的膨胀图形。我们将这四个“瓦片”重新排列，将它们分别放置在新画布的上、下、左、右四个方位，形成一个中心重叠的十字形状。
    • 难点：新画布的尺寸 a_pic 以及四个“瓦片”的精确放置坐标，是这一步的关键。通过观察和推演，我发现了一个至关重要的递推规律。

关键发现：b[i-3] 递推规律

在重组阶段，各项参数的计算并非无迹可寻。我发现，当进行第 i 次演变（i 为偶数且 i >= 4）时，新画布的尺寸以及重叠的深度，都与第 i-3 次演变完成时的画布边长 b[i-3] 存在一个确定的数学关系。

下图为做题时的手绘示意图，可供直观理解：

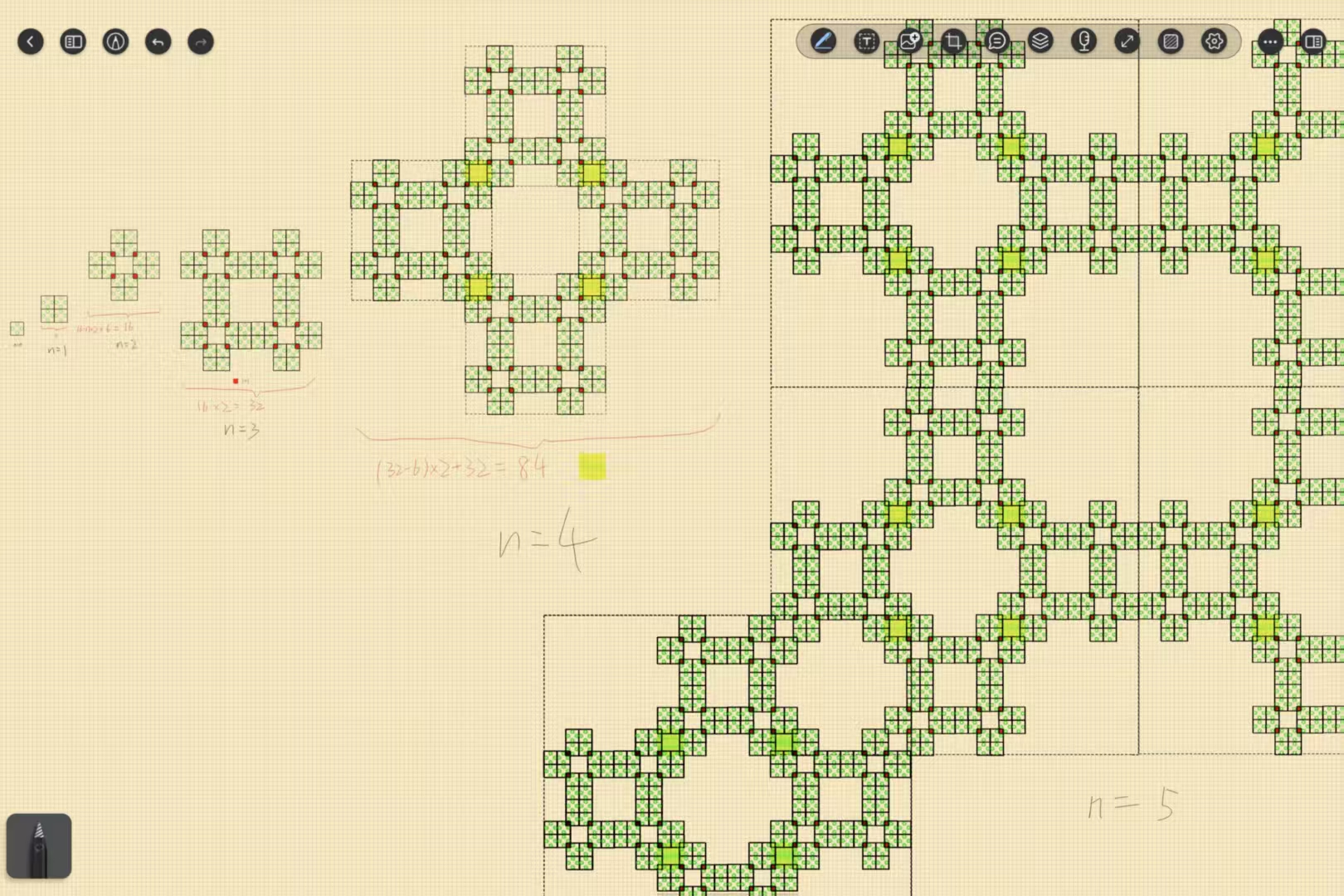
  • 新画布尺寸 a_pic 的计算 (update_a 函数):
    a_pic(i) = a_pic(i-1) + (a_pic(i-1) - b[i-3]) * 2
    这里的 a_pic(i-1) 是上一个奇数膨胀阶段的边长。这个公式描述了新画布如何在上一阶段的基础上，根据 i-3 步的历史状态进行扩张。

  • 布局坐标的计算 (draw 函数):
    在 draw 函数中，放置“瓦片”的起始坐标偏移量，也由 b[i-3] 决定。例如，左侧瓦片的 y 坐标和上方瓦片的 x 坐标，都涉及到一个关键偏移量：a_temp - (b[i - 3] - 1)，其中 a_temp 是 a_pic(i-1)。

这个递推关系，正是图形演变过程的关键。它将一个复杂的几何问题，转化为了一个可以通过历史数据精确计算的数学问题。i=2 的情况由于 i-3 无意义，需要作为特殊情况单独处理。

可行性分析

  • 时间复杂度:

    • 外层循环执行 n 次。在每次循环内部，核心操作是 draw 函数，它本质上是数组的复制，复杂度为 O(a_temp^2)。
    • 画布边长 a_pic 大致以 2*sqrt(2) 为公比的等比数列增长（奇数步*2，偶数步*sqrt(2)左右）。当 n 较小时，a_pic 的增长在可控范围内，对于题目数据范围，总计算量可以接受。

  • 空间复杂度:

    • 我们需要 pic 和 temp 两个二维数组来存储图形，其大小由最终的 a_pic 决定。空间复杂度为 O(a_pic^2)。

  • 结论：
    该算法将复杂的图形生成问题转化为迭代计算，通过发现递推规律避免了复杂的几何推导，方案可行。

实现

基于以上思路，我构建了最终的AC代码。它通过 pic 和 temp 两个数组作为双缓冲，交替进行图形的生成和暂存，并通过 update_a 和 draw 函数，精确实现了奇偶交替的演变逻辑。

点击展开/折叠 最终AC代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include<bits/stdc++.h>
using namespace std;
int const maxn = 1e3 + 5;

int n, a_pic = 3, a_temp = 3, b[10];
char pic[maxn][maxn];
char temp[maxn][maxn];

bool isEven(int num){
	return !(num & 1);
}

void draw(int x, int y){
	for(int i = 1; i <= a_temp; ++i){
		for(int j = 1; j <= a_temp; ++j){
			if(pic[x + i - 1][y + j - 1] != 'o'){
				pic[x + i - 1][y + j - 1] = temp[i][j];
			}
		}
	}
}

void update_a(int x){
	if(!isEven(x)){
		a_pic *= 2;
		b[x] = a_pic;
	}
	else{
		if(x == 2){
			a_pic = a_temp * 3 - 2;
		}
		else{
			a_pic = a_pic + (a_pic - b[x - 3]) * 2;
		}
	}
}

void update_temp(){
	for(int i = 1; i <= a_pic; ++i){
		for(int j = 1; j <= a_pic; ++j){
			if (pic[i][j] == 0) {
				pic[i][j] = ' ';
			}
			temp[i][j] = pic[i][j];
		}	
	}
	a_temp = a_pic;
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	temp[1][1] = ' ', temp[1][2] = 'o', temp[1][3] = ' ', temp[2][1] = 'o', temp[2][2] = ' ', temp[2][3] = 'o', temp[3][1] = ' ', temp[3][2] = 'o', temp[3][3] = ' ';
	cin >> n;
	if(n == 0){
		for(int i = 1; i <= 3; ++i){
			for(int j = 1; j <= 3; ++j){
				cout << " " << temp[i][j];
			}
			cout << '\n';
		}
		return 0;
	} 
	for(int i = 1; i <= n; ++i){
		update_a(i);
		for (int j = 1; j <= a_temp; ++j) {
			memset(pic[j], 0, sizeof pic[j]);
		}
		if(!isEven(i)){
			draw(1, 1);
			draw(1, 1 + a_temp);
			draw(1 + a_temp, 1);
			draw(1 + a_temp, 1 + a_temp);
		}
		else{
			if(i == 2){
				draw(1, a_temp);
				draw(a_temp, 1);
				draw(a_temp, 2 * a_temp - 1);
				draw(2 * a_temp - 1, a_temp);
			}
			else{
				draw(1, a_temp - (b[i - 3] - 1));
				draw(a_temp - (b[i - 3] - 1), 1);
				draw(a_temp - (b[i - 3] - 1), 2 * a_temp - (2 * b[i - 3] - 1));
				draw(2 * a_temp - (2 * b[i - 3] - 1), a_temp - (b[i - 3] - 1));
			}
		}
		update_temp();
	}
	for(int i = 1; i <= a_pic; ++i){
		for(int j = 1; j <= a_pic; ++j){
			cout << " " << pic[i][j];
		}
		cout << '\n';
	}
	return 0;
}

各阶段图形演变

为了直观地展示算法的最终效果以及图形的演变之美，以下是 n=0 到 n=6 的完整输出图形。

点击展开/折叠 n=0 的输出图形
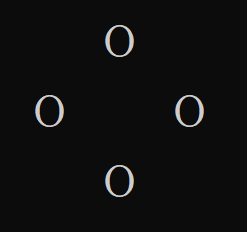
点击展开/折叠 n=1 的输出图形
点击展开/折叠 n=2 的输出图形
点击展开/折叠 n=3 的输出图形
点击展开/折叠 n=4 的输出图形
点击展开/折叠 n=5 的输出图形
点击展开/折叠 n=6 的输出图形

总结

  1. 分解操作步骤：解决本题的第一步，是将题目描述的单次复杂操作，拆解为奇数步膨胀和偶数步重组这两个逻辑更清晰、更容易实现的交替步骤。
  2. 寻找递推规律：对于复杂的模拟题，直接推导通项公式往往很困难。本题的突破口在于观察并发现了控制图形尺寸和坐标的递推关系（b[i-3]规律），这比纯粹的几何分析要直接得多。
  3. 迭代与双缓冲：采用迭代的方式，一步步从初始状态构建出最终图形，是解决此类问题的稳妥方法。使用 pic 和 temp 两个数组作为双缓冲，可以很方便地根据前一阶段的图形来生成下一阶段，避免了数据的原地修改冲突。