洛谷-P1133-教主的花园·复盘——从线性DP到环形DP

发表于 更新于 分类于

前言

最近，我解决了一道经典的 环形DP 问题。该问题具有较强的迷惑性，我设计了一个看似正确的线性DP模型，实际上忽略了问题最核心的 环形 约束。本文旨在完整复盘从一个70分的线性解，到一个90分的 错误补丁 解，最终到100分AC的 破环成链 正解的全过程，深入剖析每一步的思维误区与正确建模的关键。

题目分析

P1133 教主的花园

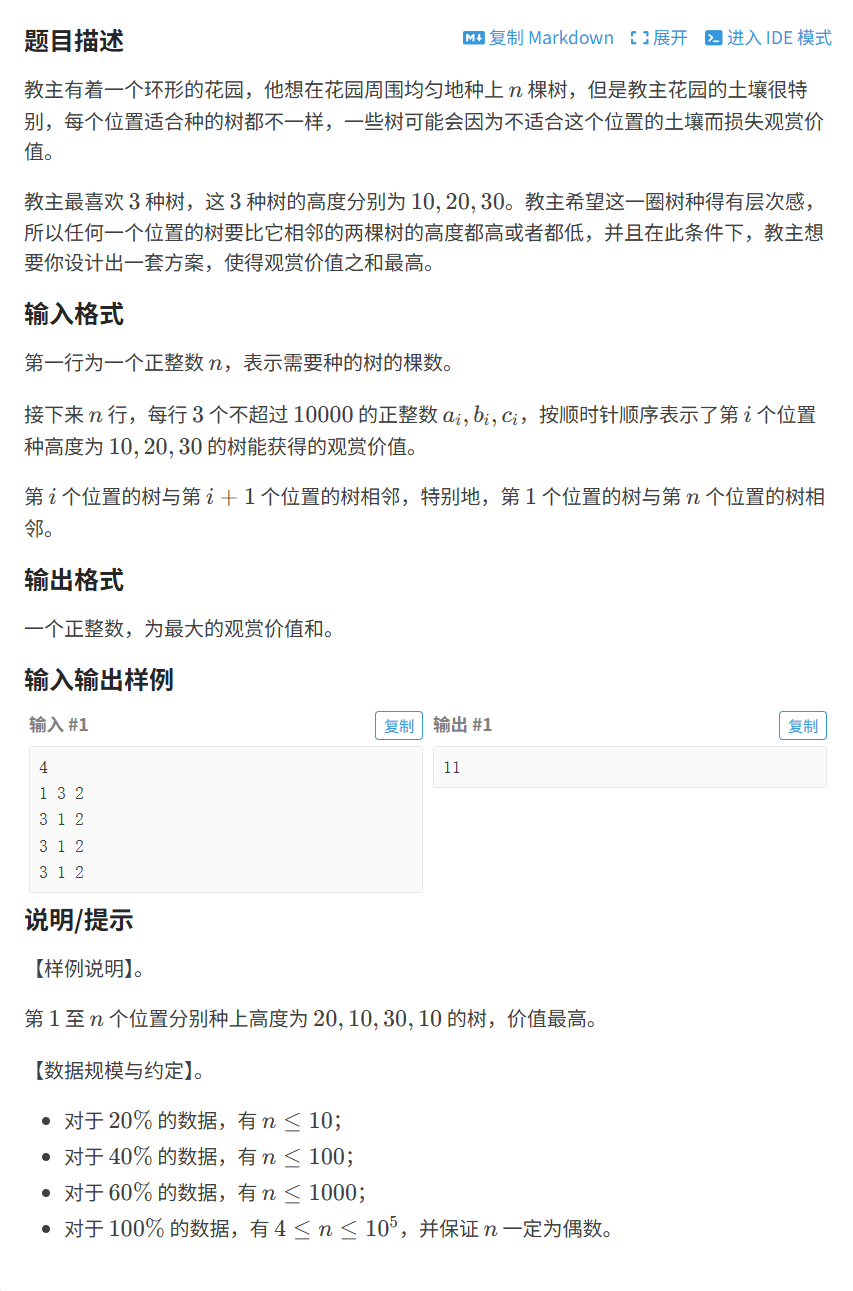
提炼题目要素：

  1. 布局：环形 排列。
  2. 约束：任何一棵树必须比其左右相邻的树 同时更高或更矮，形成 波峰 或 波谷。
  3. 目标：观赏价值总和最大。

这是一个动态规划问题。核心在于状态的设计。为了存储输入的观赏价值，我使用了一个 Plant_Position 结构体，其中 pos[i].ten, pos[i].twenty, pos[i].thirty 持有位置 i 的相应价值。

为了判断位置 i 的种植是否合法，不仅需要知道位置 i-1 的高度，还需要知道 i-1 相对于 i-2 的趋势，这样才能决定 i 的合法走向。因此，一个三维状态是必要的：dp[i][j][k]。

  • i：表示正在考虑第 i 棵树。
  • j：表示第 i 棵树的高度。我们用 1, 2, 3 分别代表高度 10, 20, 30。
  • k：表示第 i 棵树的形态。
    • k=0：第 i 棵树是 波谷，即 H[i-1] > H[i]，从 i-1 到 i 是 下降 趋势。
    • k=1：第 i 棵树是 波峰，即 H[i-1] < H[i]，从 i-1 到 i 是 上升 趋势。

dp[i][j][k] 的值，就代表满足以上定义时的最大观赏价值。

算法设计及实现

V1.0 线性DP的初步尝试 (70分)

设计

最初的方案完全忽略了 环形 约束，将花园视为一个从 1 到 n 的 线性序列。基于上述 dp[i][j][k] 状态，可以推导出所有合法的状态转移方程。

状态转移方程详解：

  1. 目标状态: dp[i][1][0] (高度 10 , 波谷/下降)

    • 逻辑: 要下降到高度 10 ，前一个位置 i-1 的高度必须是 20 或 30 。同时，为了形成波谷，前一个位置 i-1 必须是波峰（上升趋势，k=1）。
    • 方程: dp[i][1][0] = max(dp[i-1][2][1], dp[i-1][3][1]) + pos[i].ten

  2. 目标状态: dp[i][2][0] (高度 20 , 波谷/下降)

    • 逻辑: 要下降到高度 20 ，前一个位置 i-1 的高度必须是 30 。前一个位置 i-1 必须是波峰（上升趋势，k=1）。
    • 方程: dp[i][2][0] = dp[i-1][3][1] + pos[i].twenty

  3. 目标状态: dp[i][2][1] (高度 20 , 波峰/上升)

    • 逻辑: 要上升到高度 20 ，前一个位置 i-1 的高度必须是 10 。前一个位置 i-1 必须是波谷（下降趋势，k=0）。
    • 方程: dp[i][2][1] = dp[i-1][1][0] + pos[i].twenty

  4. 目标状态: dp[i][3][1] (高度 30 , 波峰/上升)

    • 逻辑: 要上升到高度 30 ，前一个位置 i-1 的高度可以是 10 或 20 。前一个位置 i-1 必须是波谷（下降趋势，k=0）。
    • 方程: dp[i][3][1] = max(dp[i-1][1][0], dp[i-1][2][0]) + pos[i].thirty

不可达状态:

  • dp[i][1][1] (上升到最低点) 和 dp[i][3][0] (下降到最高点) 是不可能出现的。这些状态的值应保持为极小值，不参与计算。

实现

该方案的实现直接从 i=1 循环到 n，并在最后取 dp[n] 所有合法状态的最大值作为结果。

70分提交记录

点击展开/折叠 V1.0 70分代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][8][7];
Plant_Position pos[maxn];

void dp_10_0(int idx) {
    dp[idx][1][0] = max(dp[idx - 1][2][1], dp[idx - 1][3][1]) + pos[idx].ten;
}

void dp_20_0(int idx) {
    dp[idx][2][0] = dp[idx - 1][3][1] + pos[idx].twenty;
}

void dp_20_1(int idx) {
    dp[idx][2][1] = dp[idx - 1][1][0] + pos[idx].twenty;
}

void dp_30_1(int idx) {
    dp[idx][3][1] = max(dp[idx - 1][1][0], dp[idx - 1][2][0]) + pos[idx].thirty;
}

ll DP() {
    for (int i = 1; i <= n; i++) {
        dp_10_0(i);
        dp_20_0(i);
        dp_20_1(i);
        dp_30_1(i);
    }
    return max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    cout << DP();
    return 0;
}

错误分析

  • 问题根源：
    该方案计算出的结果是 线性排列 下的最优解。但题目要求的是 环形排列。线性最优解的第 n 个位置和第 1 个位置的状态，很可能不满足高低交错的约束，因此该解对于环形问题是 非法的。

V2.0 “打补丁”的错误修正 (90分)

设计

在提交V1.0后，我意识到了环形约束的问题。此时产生了一个错误的修正思路：先算出线性最优，再检查它是否满足环形约束。

这个思路最初的实现是一个复杂且繁琐的 while 循环：

点击展开/折叠 while“补丁” 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
ans.push_back(dp[n][1][0]);
ans.push_back(dp[n][2][0]);
ans.push_back(dp[n][2][1]);
ans.push_back(dp[n][3][1]);
sort(ans.begin(), ans.end());
bool y[5] = {0};
while (1) {
    if (ans.back() == dp[n][2][0] && !y[0]) {
        if (pos[1].twenty < pos[1].thirty) {
            cout << ans.back();
            return;
        }
        else {
            y[0] = true;
            ans.pop_back();
            continue;
        }
    }
    if (ans.back() == dp[n][2][1] && !y[1]) {
        if (pos[1].twenty < pos[1].ten) {
            cout << ans.back();
            return;
        }
        else {
            y[1] = true;
            ans.pop_back();
            continue;
        }
    }
    cout << ans.back();
    return;
}

这个复杂的 while 最终被我精简为两个 if 语句：

1
2
3
4
5
6
7
if (pos[1].twenty > pos[1].ten) {
    dp[n][2][1] = 0;
}
if (pos[1].twenty > pos[1].thirty) {
    dp[n][2][0] = 0;
}
cout << max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));

if 虽比 while 精简了很多，其内在的错误逻辑是相同的。这个 “补丁” 的意图是，从线性DP算出的几个最优候选解中，通过一套逻辑来 推断 并 验证 起点是否合法。

其验证逻辑如下：

  1. 无约束情况：如果线性最优解的终点是 dp[n][1][0] ( H=10 , 下降) 或 dp[n][3][1] ( H=30 , 上升)，则直接接受。

    • 推断: 如果 H[n]=10，则环要求 H[1] > 10，即 H[1] 可以是 20 或 30 。因为有两个选择，代码便假设总能找到一个合法的起点，无需干预。H[n]=30 同理。

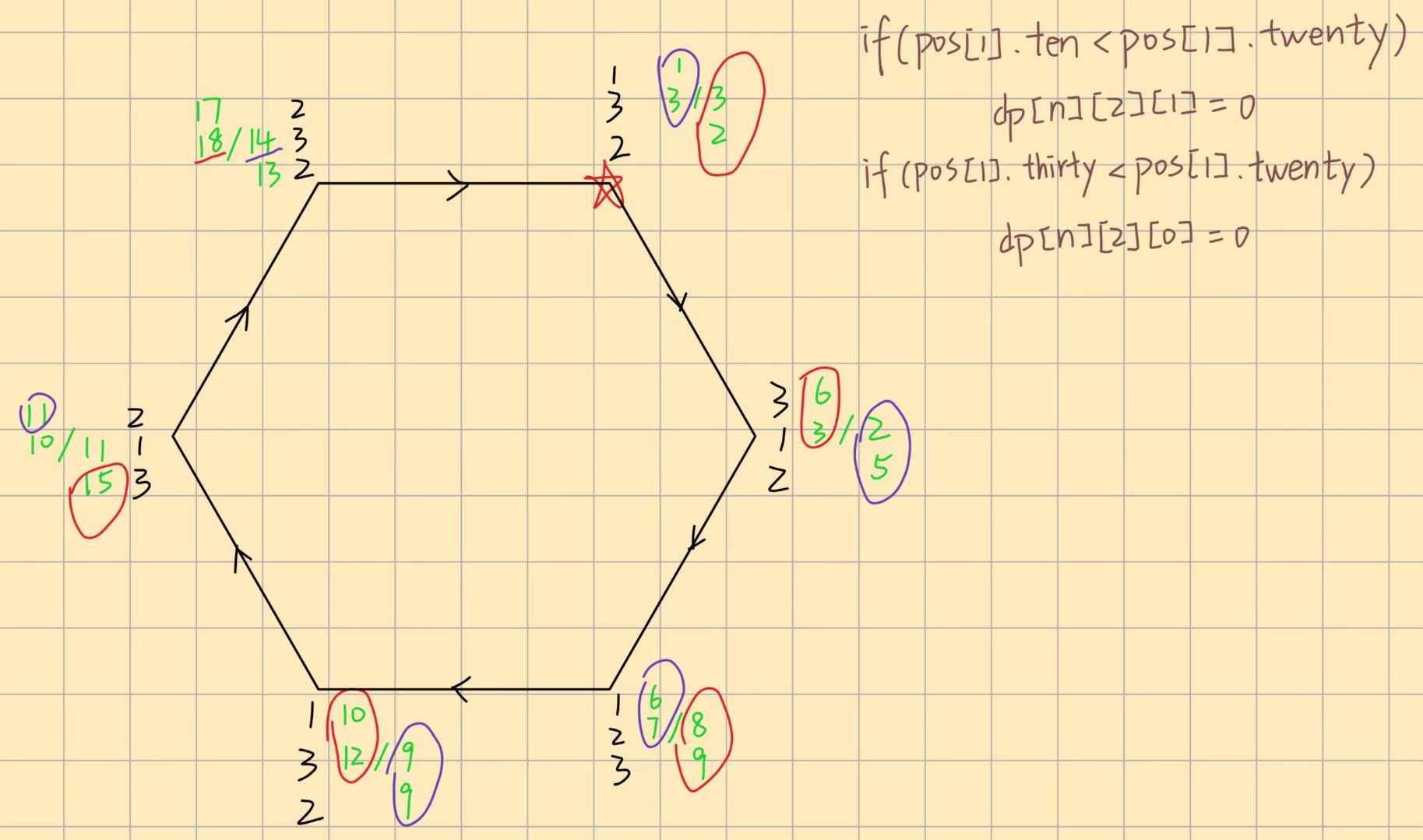
  2. 约束情况 1: 当考虑终点为 dp[n][2][1] ( H=20 , 上升) 的路径时。

    • 推断: 这个终点状态意味着 H[n-1]=10。为了构成环，H[1] 必须小于 H[n]=20，所以 H[1] 必须是 10。
    • 验证: 此时，代码进行一次 贪心 检查：if (pos[1].twenty > pos[1].ten)。这个判断的逻辑是：“如果在起点上，种 20 的观赏价值比种 10 要高，那么一个真正最优的路径，当初在起点时就 不可能 选择种 10 ”。基于这个贪心假设，如果条件成立，就认为这条要求起点为 10 的路径不可能是最优解，于是通过 dp[n][2][1] = 0 将其作废。

  3. 约束情况 2: 当考虑终点为 dp[n][2][0] ( H=20 , 下降) 的路径时。

    • 推断: 这个终点状态意味着 H[n-1]=30。为了构成环，H[1] 必须大于 H[n]=20，所以 H[1] 必须是 30。
    • 验证: 类似地，代码进行贪心检查 if (pos[1].twenty > pos[1].thirty)。如果种 20 的价值更高，就认为这条要求起点为 30 的路径不可能是最优解，将其作废。

实现

90分提交记录

点击展开/折叠 V2.0 代码 (90分) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][8][7];
Plant_Position pos[maxn];
vector<ll> ans;

void dp_10_0(int idx) {
    dp[idx][1][0] = max(dp[idx - 1][2][1], dp[idx - 1][3][1]) + pos[idx].ten;
}

void dp_20_0(int idx) {
    dp[idx][2][0] = dp[idx - 1][3][1] + pos[idx].twenty;
}

void dp_20_1(int idx) {
    dp[idx][2][1] = dp[idx - 1][1][0] + pos[idx].twenty;
}

void dp_30_1(int idx) {
    dp[idx][3][1] = max(dp[idx - 1][1][0], dp[idx - 1][2][0]) + pos[idx].thirty;
}

void DP() {
    for (int i = 1; i <= n; i++) {
        dp_10_0(i);
        dp_20_0(i);
        dp_20_1(i);
        dp_30_1(i);
    }
    if (pos[1].twenty > pos[1].ten) {
        dp[n][2][1] = 0;
    }
    if (pos[1].twenty > pos[1].thirty) {
        dp[n][2][0] = 0;
    }
    cout << max(max(dp[n][1][0], dp[n][3][1]), max(dp[n][2][0], dp[n][2][1]));
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    DP();
    return 0;
}

错误分析

  • 根本性缺陷：
    此方案的失败，并非因为 if 语句这个 补丁 本身不够精巧。恰恰相反，它很好地浓缩了前一版 while 循环的意图，是一个逻辑上很优质的补丁。

    真正的错误出在算法的 根本设计 上。这种 事后补救 的方法，就相当于把一条通往错误方向的道路修得非常漂亮，但道路再好，也无法到达正确的终点。

    其核心谬误在于，它错误地假设了 环形最优解一定包含在线性最优解之中。而事实上，真正的环形最优解，其线性部分可能根本不是最优的。代码只检查了少数几个 线性最优 的候选者，而真正的答案可能在第一次DP时，就因为在线性排列上得分不够高而被直接淘汰，永远没有机会被最后的 if 语句检查。这是一种典型的 局部最优陷阱。

V3.0 “破环成链”的正确解法 (AC)

设计

正确的做法是放弃 事后补救，采用处理环形问题的 标准范式——破环成链。

其核心思想是，将一个复杂的环形问题，分解为几个独立的、带有明确起始和结束约束 的线性问题。

具体方案是，通过一个外层循环，强制指定 第 1 棵树 的高度（分三种情况： H=10 , H=20 , H=30 ）。对每种情况独立进行一次从2到n的线性DP，并在最后根据固定的起点，对终点 dp[n] 的状态进行合法性筛选。

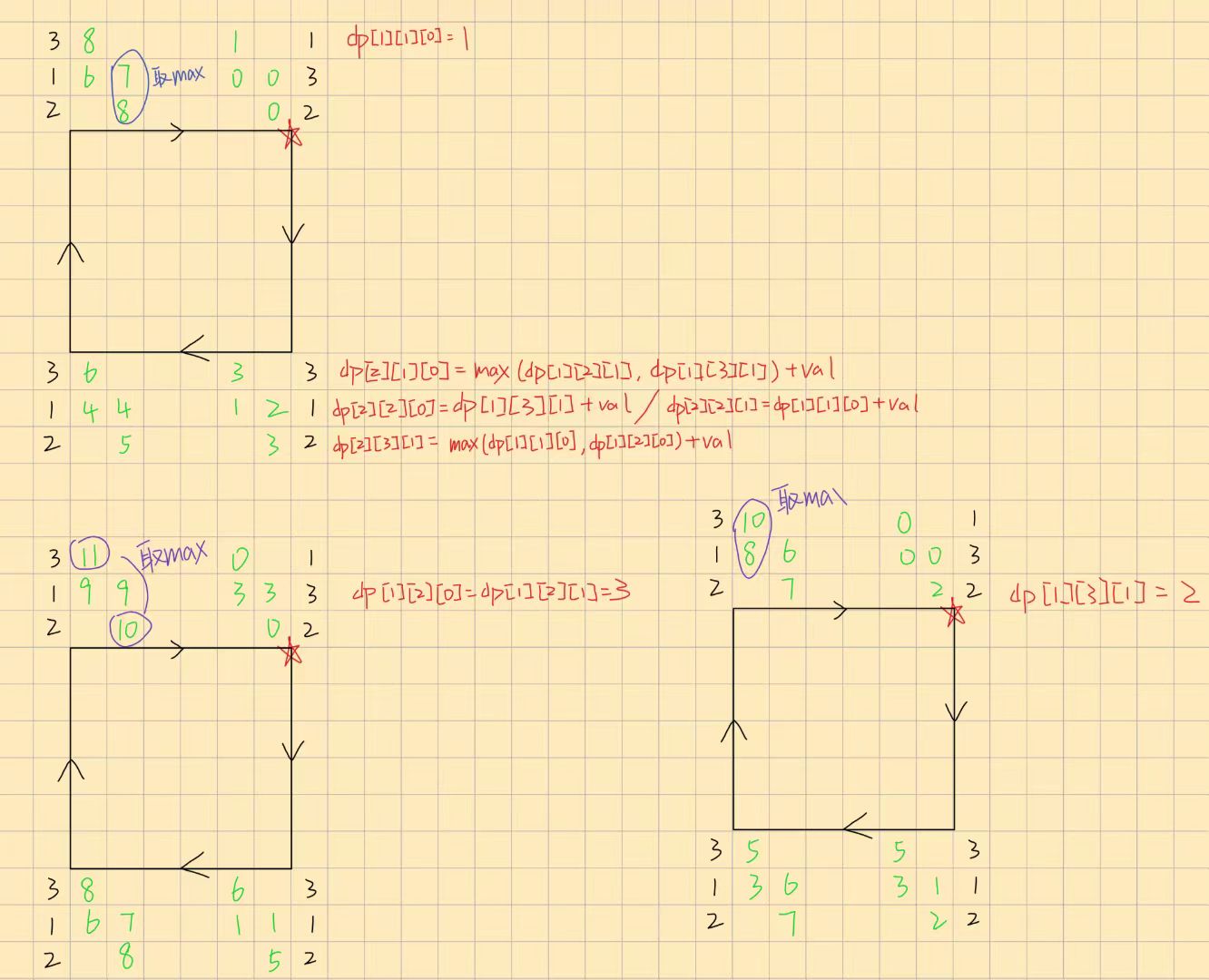
可行性分析

  • 时间复杂度: 每次DP的计算量是 O(n)。总共进行3次独立的DP，所以总时间复杂度依然是 O(n)。
  • 空间复杂度: O(n)。
  • 结论: 方案高效可行。

实现

AC提交记录

点击展开/折叠 V3.0 AC代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 1e5 + 5;

struct Plant_Position {
    ll ten, twenty, thirty;
};

ll n, dp[maxn][5][5], ans;
Plant_Position pos[maxn];

void DP() {
    ll ans = 0;
    for (int i = 1; i <= 3; i++) {
        if (i == 1) {
            dp[1][1][0] = pos[1].ten;
        }
        else if (i == 2) {
            dp[1][2][0] = pos[1].twenty, dp[1][2][1] = pos[1].twenty;
        }
        else if (i == 3) {
            dp[1][3][1] = pos[1].thirty;
        }
        for (int i = 2; i <= n; i++) {
            dp[i][1][0] = max(dp[i - 1][2][1], dp[i - 1][3][1]) + pos[i].ten;
            dp[i][2][0] = dp[i - 1][3][1] + pos[i].twenty;
            dp[i][2][1] = dp[i - 1][1][0] + pos[i].twenty;
            dp[i][3][1] = max(dp[i - 1][1][0], dp[i - 1][2][0]) + pos[i].thirty;
        }
        if (i == 1) {
            ans = max(ans, max(dp[n][2][1], dp[n][3][1]));
        }
        else if (i == 2) {
            ans = max(ans, max(dp[n][1][0], dp[n][3][1]));
        }
        else if (i == 3) {
            ans = max(ans, max(dp[n][1][0], dp[n][2][0]));
        }
        memset(dp, 0, sizeof(dp));
    }
    cout << ans;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> pos[i].ten >> pos[i].twenty >> pos[i].thirty;
    }
    DP();
    return 0;
}

  • 实现细节剖析
    该方案的精髓在于，将环形约束从一个 事后检查 的难题，转化为了一个 顶层设计 的分类讨论。在固定了起点后，最后结算时对终点的筛选逻辑如下：

    1. 若起点 H[1]=10 (波谷):

      • 为构成环，终点 H[n] 必须是波峰，且 H[n] > H[1]。
      • 合法终点状态：dp[n][2][1] ( H=20 , 上升) 和 dp[n][3][1] ( H=30 , 上升)。
      • 候选答案: max(dp[n][2][1], dp[n][3][1])

    2. 若起点 H[1]=20 (波峰或波谷):

      • 为构成环，若 H[n] 是波峰，则 H[n] > H[1]；若 H[n] 是波谷，则 H[n] < H[1]。
      • 合法终点状态：dp[n][3][1] ( H=30 , 上升) 和 dp[n][1][0] ( H=10 , 下降)。
      • 候选答案: max(dp[n][3][1], dp[n][1][0])

    3. 若起点 H[1]=30 (波峰):

      • 为构成环，终点 H[n] 必须是波谷，且 H[n] < H[1]。
      • 合法终点状态：dp[n][1][0] ( H=10 , 下降) 和 dp[n][2][0] ( H=20 , 下降)。
      • 候选答案: max(dp[n][1][0], dp[n][2][0])

    最终答案就是这三个候选答案中的最大值。这种精确的筛选保证了最终解的合法性。

总结

  1. 问题建模是关键：正确识别并处理 环形 这一核心模型，是解决本题的钥匙。直接套用线性模型会导致从根本上偏离题意。
  2. 警惕“打补丁”式的修正：当发现算法有漏洞时，复杂的 事后检查 逻辑往往是错误或不完备的。正确的做法是回到设计的起点，思考如何将约束从一开始就融入算法模型。
  3. 掌握标准范式：破环成链 是解决几乎所有环形DP、环形数组问题的通用且强大的思想，必须熟练掌握。