洛谷-P1121-环状最大两段子段和·复盘——续谈环形DP

发表于 2025-11-03 分类于算法题解/复盘

前言

本文复盘洛谷 P1121 环状最大两段子段和 的解题过程。本次复盘的核心算法思路，即 分类讨论 结合 对偶思想，在初版实现中就是正确的。然而，一个由非空约束导致的边界情况，使得初版代码无法通过全部测试点。本文将详细分析该边界情况的触发机理，并展示如何通过一行代码进行修复，将80分的实现修正为100分的最终解。

题目分析

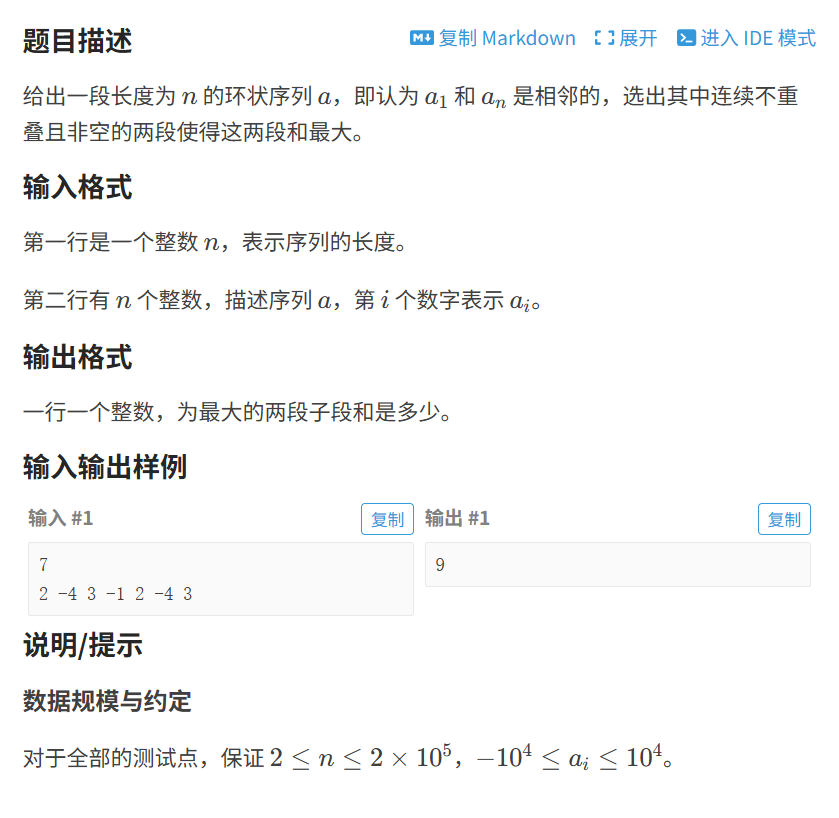
提炼题目要素：

布局：环形排列。a[1] 和 a[n] 相邻。这意味着一个连续子段可以从数组尾部跨越到头部。
目标：选出两段 不重叠 且非空的连续子段，使其和最大。非空约束是处理边界情况的关键。
约束：N最大为2e5，算法的时间复杂度必须是O(N)或O(N log N)。

此问题需要在环形结构上求解两段子段的和的最大值。重点在于设计一个线性时间复杂度的算法，以处理 环形结构 和 两段选择 的双重约束。

算法设计及实现

V1.0 初版实现 (80分)

设计

在环形结构上直接进行动态规划，因其缺少固定起终点而难以定义状态。因此，采用标准方法，将环形问题分解为线性问题进行处理。

对所有可能的两段子段的选择，按其是否跨越 a[1] 和 a[n] 的连接点，可分为两种情况：

情况一：选择的两段不跨越 a[1]-a[n] 的连接点。
- 问题转化: 此情况等价于在链 a[1...n] 上寻找最大两段子段和。
- 解决方案: 通过枚举分割点来解决。链上的两段最优解 S1 和 S2 之间必定存在一个分割点。
  a. 通过动态规划预处理计算两个辅助数组：
  - max_L_to_R[i]：存储 前缀区间 a[1...i] 内的最大单段子段和。
  - max_R_to_L[i]：存储 后缀区间 a[i...n] 内的最大单段子段和。
    b. 遍历所有可能的分割点 i (1 到 n-1)，计算 max_L_to_R[i] + max_R_to_L[i+1]。
    c. 这些和中的最大值，即为情况一的解。

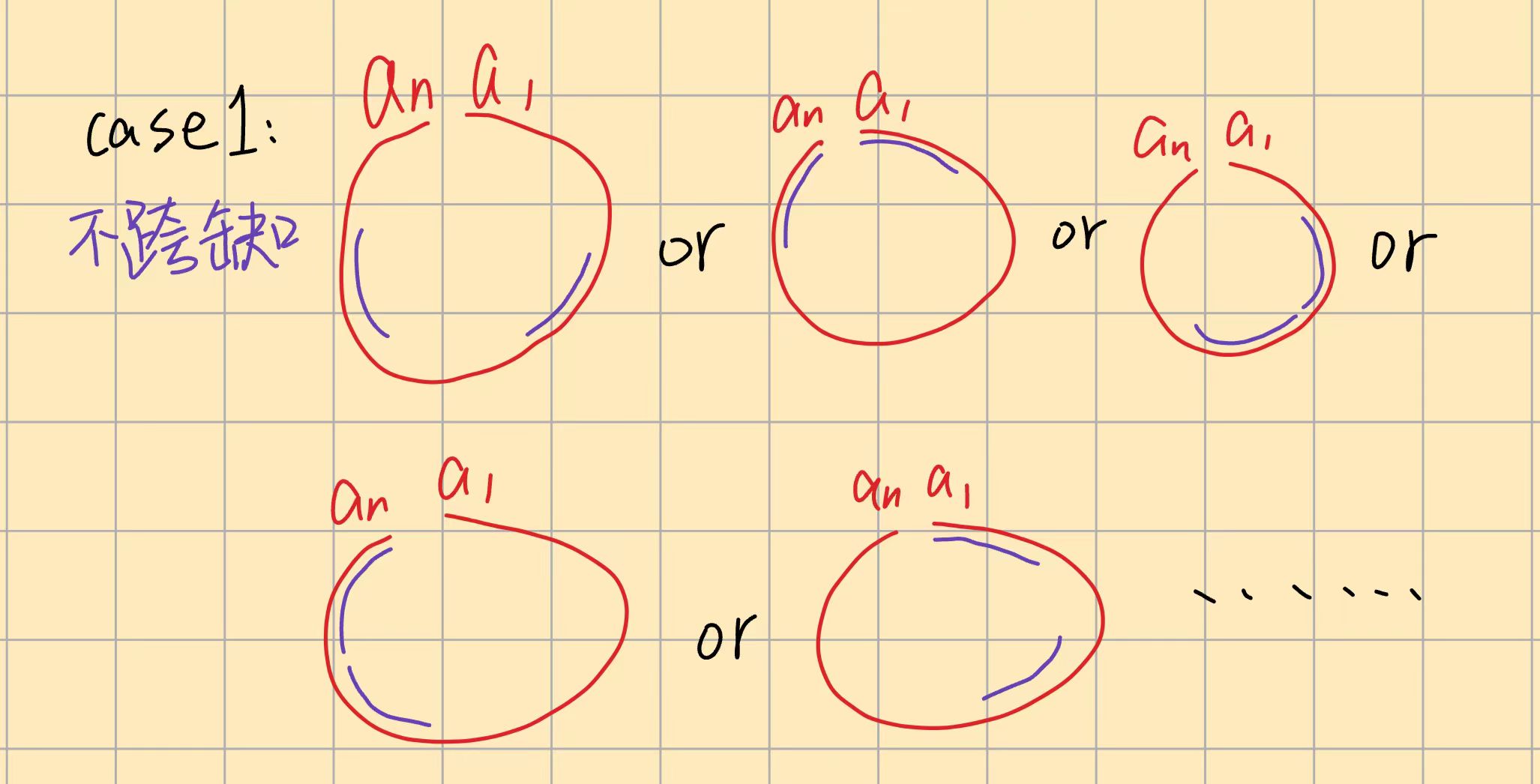
情况二：选择的两段跨越 a[1]-a[n] 的连接点。
- 问题转化: 此情况指一段位于数组尾部，另一段位于头部。为简化计算，采用对偶思想。
- 逻辑原理: (选中元素的和) = (数组总和) - (未选中元素的和)。
- 核心观察: 若选中的部分是跨界的，则未选中的部分必然是 不跨界 的。
- 再次转化: 最大化 选中元素的和，等价于最小化 未选中元素的和。
- 解决方案:
  a. 问题转化为：在链 a[1...n] 上，寻找 最小两段子段和。
  b. 采用与情况一对称的方法，计算 min_L_to_R 和 min_R_to_L 数组，求出链上的最小两段和。
  c. 用 数组总和 减去此值，即为情况二的解。

最终答案为 max(情况一的解, 情况二的解)。该算法的时间复杂度为O(N)。

实现

80分提交记录

点击展开/折叠 V1.0 80分代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 2e5 + 5, minn = -1e9;

int n;
ll total_a, a[maxn], max_L_to_R[maxn], dp_max_L_to_R[maxn], max_R_to_L[maxn], dp_max_R_to_L[maxn], min_L_to_R[maxn], dp_min_L_to_R[maxn], min_R_to_L[maxn], dp_min_R_to_L[maxn];

void find_L_to_R() {
    ll max_val = minn, min_val = maxn;
    for (int i = 1; i <= n; ++i) {
        dp_max_L_to_R[i] = max(dp_max_L_to_R[i - 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_L_to_R[i]);
        max_L_to_R[i] = max_val;
        dp_min_L_to_R[i] = min(dp_min_L_to_R[i - 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_L_to_R[i]);
        min_L_to_R[i] = min_val;
    }
}

void find_R_to_L() {
    ll max_val = minn, min_val = maxn;
    for (int i = n; i >= 1; --i) {
        dp_max_R_to_L[i] = max(dp_max_R_to_L[i + 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_R_to_L[i]);
        max_R_to_L[i] = max_val;
        dp_min_R_to_L[i] = min(dp_min_R_to_L[i + 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_R_to_L[i]);
        min_R_to_L[i] = min_val;
    }
}

ll case_1() {
    ll max_val = minn;
    for (int i = 1; i < n; ++i) {
        max_val = max(max_val, max_L_to_R[i] + max_R_to_L[i + 1]);
    }
    return max_val;
}

ll case_2() {
    ll min_val = maxn;
    for (int i = 1; i < n; ++i) {
        min_val = min(min_val, min_L_to_R[i] + min_R_to_L[i + 1]);
    }
    return total_a - min_val;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        total_a += a[i];
    }
    find_L_to_R();
    find_R_to_L();
    cout << max(case_1(), case_2());
    return 0;
}

错误分析

问题根源：
算法的理论模型正确，但代码实现未处理一个由非空约束引发的特殊情况。该问题在输入数组 全为负数 的测试点上触发。
错误原因：
1. 当数组全为负数时，为使和最小，算法会选择尽可能多的元素。因此，计算出的 链上最小两段和 等于 数组总和。
2. 此时，case_2() 函数的计算 total_a - min_val 变为 total_a - total_a，结果为 0。
3. 根据非空约束，对于全负数组，任意两段非空子段的和必须为负数。case_1() 会正确计算出这个负数的最优解。
4. 最终，main 函数在 max(一个正确的负数, 0) 的比较中，会错误地选择 0。
5. 这个结果 0 对应于 未选中全部元素 的情况，即 选中了空集，这与题目的非空约束相悖。

V2.0 修正实现 (AC)

设计

问题已明确：当 链上最小两段和 == 数组总和 时，case_2() 会产生一个违反约束的无效解 0。

修正的目标是：识别此情况，并确保该无效解不被选为最终答案。

解决方案: 修改 case_2() 函数的返回值。当 total_a == min_val 的条件成立时，函数不返回 0，而是返回一个理论上的极小值 LLONG_MIN。
效果: 任何合法的解（即使是负数）都必然大于 LLONG_MIN。因此，在最终的 max 比较中，case_1() 计算出的合法解会自动取代 case_2() 返回的 LLONG_MIN，从而保证结果的正确性。

实现

AC提交记录

点击展开/折叠 V2.0 AC代码

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
ll const maxn = 2e5 + 5;

int n;
ll total_a, a[maxn], max_L_to_R[maxn], dp_max_L_to_R[maxn], max_R_to_L[maxn], dp_max_R_to_L[maxn], min_L_to_R[maxn], dp_min_L_to_R[maxn], min_R_to_L[maxn], dp_min_R_to_L[maxn];

void find_L_to_R() {
    ll max_val = LLONG_MIN, min_val = LLONG_MAX;
    for (int i = 1; i <= n; ++i) {
        dp_max_L_to_R[i] = max(dp_max_L_to_R[i - 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_L_to_R[i]);
        max_L_to_R[i] = max_val;
        dp_min_L_to_R[i] = min(dp_min_L_to_R[i - 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_L_to_R[i]);
        min_L_to_R[i] = min_val;
    }
}

void find_R_to_L() {
    ll max_val = LLONG_MIN, min_val = LLONG_MAX;
    for (int i = n; i >= 1; --i) {
        dp_max_R_to_L[i] = max(dp_max_R_to_L[i + 1] + a[i], a[i]);
        max_val = max(max_val, dp_max_R_to_L[i]);
        max_R_to_L[i] = max_val;
        dp_min_R_to_L[i] = min(dp_min_R_to_L[i + 1] + a[i], a[i]);
        min_val = min(min_val, dp_min_R_to_L[i]);
        min_R_to_L[i] = min_val;
    }
}

ll case_1() {
    ll max_val = LLONG_MIN;
    for (int i = 1; i < n; ++i) {
        max_val = max(max_val, max_L_to_R[i] + max_R_to_L[i + 1]);
    }
    return max_val;
}

ll case_2() {
    ll min_val = LLONG_MAX;
    for (int i = 1; i < n; ++i) {
        min_val = min(min_val, min_L_to_R[i] + min_R_to_L[i + 1]);
    }
    return total_a == min_val ? LLONG_MIN : total_a - min_val;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        total_a += a[i];
    }
    find_L_to_R();
    find_R_to_L();
    cout << max(case_1(), case_2());
    return 0;
}

实现细节剖析
核心改动位于 case_2() 函数的返回语句：
return total_a == min_val ? LLONG_MIN : total_a - min_val;
该行代码使用三元运算符，将对特殊情况的判断和处理封装在函数内部，解决了问题。
健壮性提升
AC代码将所有用于初始化的极大/极小值，从硬编码的数值（如1e9）替换为标准库 <climits> 中定义的 LLONG_MAX 和 LLONG_MIN。这使代码不依赖于对题目数据范围的假设，提高了通用性和健壮性。

P.S. 完整手稿

总结

环形问题处理方法：分类讨论 结合 对偶思想 是处理此类环形数组问题的有效方法，可将问题转化为线性空间下的计算。
边界情况的重要性：必须分析全正、全负等特殊数据集。题目的非空等约束，在这些边界情况下是决定算法正确性的关键。
一种处理无效解的技巧：当算法的一个分支可能产生逻辑上无效的解时，可以使其返回一个在最终聚合操作（如max或min）中必定会被淘汰的值（如LLONG_MIN或LLONG_MAX），从而避免复杂的外部逻辑判断。