从 洛谷 P1637 三元上升子序列 到 SPOJ INCSEQ —— 长度 k 严格上升子序列的树状数组模板

发表于 更新于 分类于

前言

这篇文章记录我做 洛谷 P1637 三元上升子序列 和 SPOJ INCSEQ Increasing Subsequences 的过程，以及中途无意间发现的一套可以 通解“长度为 k 的严格上升子序列计数” 的模板。

大致路线：

  1. 先从 P1637 出发，用两棵树状数组把“三元上升子序列”写成一个非常自然的过程；
  2. 再把这套写法抽象成数学形式，发现它其实已经是一个“按长度分层 + 按值域前缀和”的 DP 框架；
  3. 在 SPOJ INCSEQ 上把这个框架推广到「任意 k」，整理成一份可以直接丢进代码库的模板。

第一部分：P1637 三元上升子序列（k = 3）

1. 题面

Luogu P1637 三元上升子序列

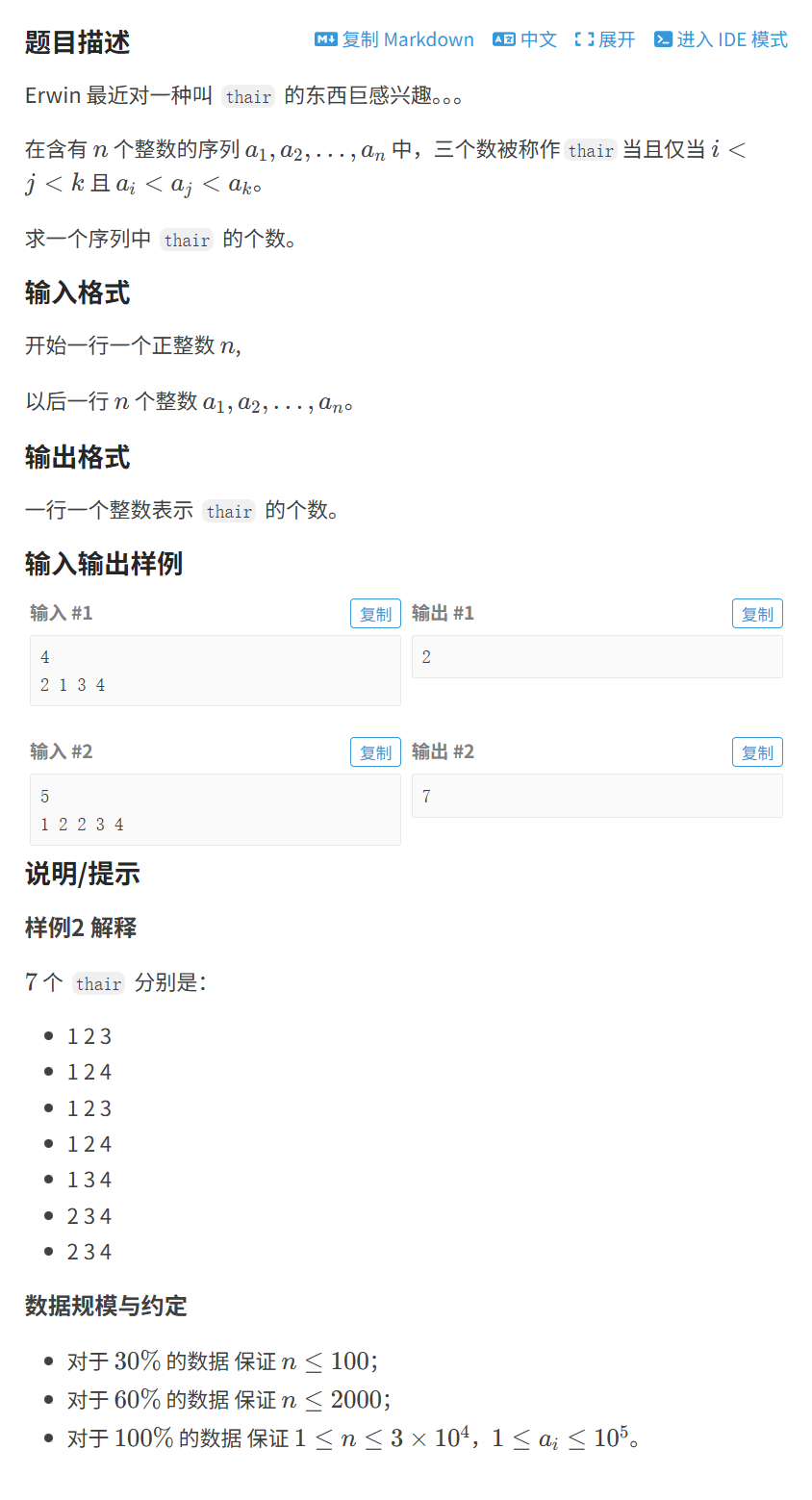
信息提炼：

  • 目标是统计三元组

    (i,j,k)s.t. i<j<k, ai<aj<ak (i, j, k)\quad \text{s.t. } i < j < k,\ a_i < a_j < a_k
  • 1≤n≤3×1041 \le n \le 3\times 10^4，值域很大，需要离散化；

  • 朴素 O(n3)O(n^3) 显然不行；

  • 即使是 “枚举中点 j，然后往左往右扫” 的 O(n2)O(n^2) 也过不了。

所以需要一个 O(nlog⁡n)O(n\log n) 级别的写法。

2. 思路：按“长度”分层，而不是按“左右”切

很多三元上升子序列的题解会强调：

  • 左边有多少个比 aja_j 小（记作 L[j]L[j]）；
  • 右边有多少个比 aja_j 大（记作 R[j]R[j]）；
  • 答案 = ∑jL[j]⋅R[j]\sum_j L[j]\cdot R[j]。

我事先并不知道这种题解里的标准做法，没有这么写，而是直接按“子序列的长度”来分层维护：

  • 长度为 1 的上升子序列：(i)(i)
  • 长度为 2 的上升子序列：(i,j)(i, j)，满足 i<j, ai<aji < j,\ a_i < a_j
  • 长度为 3 的上升子序列：(i,j,k)(i, j, k)，满足 i<j<k, ai<aj<aki < j < k,\ a_i < a_j < a_k

从左到右扫描下标 pos，当前值为 a[pos] = p 时，分三步：

  1. 把当前值当成第三个元素 kk
    • 统计所有“以前已经形成的、结尾值 < p 的长度为 2 的上升子序列”的数量；
    • 这些序列都可以接上 pp，变成长度为 3 的上升子序列；
  2. 把当前值当成第二个元素 jj
    • 统计所有“结尾值 < p 的长度为 1 的上升子序列”的数量；
    • 这些和 pp 组成长度为 2 的上升子序列；
  3. 把当前值当成第一个元素 ii
    • 自身是一个长度为 1 的上升子序列。

这背后的数学形式可以抽象成两组函数：

  • f1(v)f_1(v)：长度为 1、结尾值为 vv 的严格上升子序列个数；
  • f2(v)f_2(v)：长度为 2、结尾值为 vv 的严格上升子序列个数。

对当前值 pp（离散后下标为 idxidx），有：

长度为 3 的新增数量=∑u<pf2(u)f2(p)+=∑u<pf1(u)f1(p)+=1 \begin{aligned} \text{长度为 3 的新增数量} &= \sum_{u < p} f_2(u) \\ f_2(p) &\mathrel{+}= \sum_{u < p} f_1(u) \\ f_1(p) &\mathrel{+}= 1 \end{aligned}

整体答案就是所有“长度为 3 的新增数量”的累加。

问题变成：如何高效支持“按值域求 ∑u<pfℓ(u)\sum_{u < p} f_\ell(u)”——典型的前缀和 + 单点更新场景，直接上树状数组。

3. 离散化 & 两棵树状数组

3.1 值域离散化

因为 aia_i 值域不小，直接拿它做 BIT 下标不稳妥，先做离散化：

  1. 把所有 a[i] 放进 disperse；
  2. 排序 + 去重；
  3. 对每个 a[i] 找到它在 disperse 中的下标（从 1 开始），记作 idx。

之后所有树状数组下标都用这个 idx。

3.2 两棵 Fenwick Tree 的含义

代码中我开了两棵树：

  • cnt_op
    • 维护 f1(v)f_1(v)，即“长度为 1 的上升子序列”的计数；
    • 其实就是当前位置之前值为 vv 的元素出现次数；
  • double_pair
    • 维护 f2(v)f_2(v)，即“长度为 2 的上升子序列”的计数；
    • 记录所有以值 vv 结尾的长度为 2 的上升子序列有多少个。

于是：

  • ∑u<pf1(u)\sum_{u < p} f_1(u) 可以写成 query(idx - 1, cnt_op)；
  • ∑u<pf2(u)\sum_{u < p} f_2(u) 可以写成 query(idx - 1, double_pair)。

4. 扫描过程 & “从前往后滚”的正确性

对每个 p，离散下标 idx，按顺序执行：

  1. 当前作为第三个元素 kk
Δans=∑u<pf2(u) \Delta \text{ans} = \sum_{u < p} f_2(u) 
1
ans += query(idx - 1, double_pair);
  1. 当前作为第二个元素 jj
f2(p)+=∑u<pf1(u) f_2(p) \mathrel{+}= \sum_{u < p} f_1(u) 
1
update(idx, query(idx - 1, cnt_op), double_pair, (ll)disperse.size());
  1. 当前作为第一个元素 ii
f1(p)+=1 f_1(p) \mathrel{+}= 1 
1
update(idx, 1, cnt_op, (ll)disperse.size());

整个过程是从左到右扫描、从“长度 2”再到“长度 1”更新，看上去好像会担心“当前元素更新的结果被自己读到”。
但注意：

  • 所有 query 用的是 idx - 1；
  • Fenwick 的实现保证 query(idx - 1) 只会访问 index < idx 的位置；
  • 而 update(idx, ...) 写的是 index ≥ idx 的节点。

所以，无论是二维（P1637 的 f1/f2）还是推广到 k 维（后文），从前往后滚完全不会读到当前元素刚写入的那一格，不存在污染问题。

5. P1637 最终 AC 代码

代码完全按我自己的写法保留，用 vector + 离散化 + 两棵 Fenwick。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll maxn = 3e4 + 5;

ll n, ans;
vector<ll> a, disperse;

ll lowbit(ll x) {
    return x & -x;
}

void update(ll x, ll add, vector<ll> &tree, ll limit) {
    for (ll i = x; i <= limit; i += lowbit(i)) {
        tree[i] += add;
    }
}

ll query(ll x, vector<ll> &tree) {
    ll sum = 0;
    for (ll i = x; i; i -= lowbit(i)) {
        sum += tree[i];
    }
    return sum;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    a.reserve(maxn);
    disperse.reserve(maxn);
    cin >> n;
    for (ll i = 1; i <= n; ++i) {
        ll num;
        cin >> num;
        a.push_back(num);
        disperse.push_back(num);
    }
    sort(disperse.begin(), disperse.end());
    disperse.erase(unique(disperse.begin(), disperse.end()), disperse.end());
    vector<ll> double_pair(disperse.size() + 5, 0);
    vector<ll> cnt_op(disperse.size() + 5, 0);
    for (ll p: a) {
        ll idx = lower_bound(disperse.begin(), disperse.end(), p) - disperse.begin() + 1;
        ans += query(idx - 1, double_pair);
        update(idx, query(idx - 1, cnt_op), double_pair, (ll) disperse.size());
        update(idx, 1, cnt_op, (ll) disperse.size());
    }
    cout << ans;
    return 0;
}

（一些做题时的草稿）

到这里，P1637 这道 k=3 的问题就解决了。下面进入本文的重点：如何把这套写法推广到任意 k，并整理成模板。

第二部分：从 P1637 到通用 k 阶模板 —— INCSEQ 实战

这一部分主要做三件事：

  1. 用数学形式把上面的 P1637 写法彻底抽象；
  2. 在此基础上推广到任意长度 kk；
  3. 用 SPOJ INCSEQ 这道典型题来验证模板，并给出最终代码。

1. 抽象 P1637 的 DP 结构

先把 P1637 的写法抽象出来。

对离散后的值域 [1,m][1, m]，对所有长度 ℓ≥1\ell \ge 1，定义

fℓ(v)=长度为 ℓ，结尾值离散下标为 v 的严格上升子序列个数 f_\ell(v) = \text{长度为 }\ell\text{，结尾值离散下标为 }v\text{ 的严格上升子序列个数}

在 P1637 中：

  • f1(v)f_1(v) 存放在 cnt_op 这棵树；
  • f2(v)f_2(v) 存放在 double_pair 这棵树；
  • 每一轮扫描时，会新增一部分“长度为 3”的数量并累加到 ans，但不显式存 f3(v)f_3(v)。

对当前元素值 pp（下标 idx），转移可以统一写成：

f1(p)+=1f2(p)+=∑u<pf1(u)Ans+=∑u<pf2(u) \begin{aligned} f_1(p) &\mathrel{+}= 1 \\[4pt] f_2(p) &\mathrel{+}= \sum_{u < p} f_1(u) \\[4pt] \text{Ans} &\mathrel{+}= \sum_{u < p} f_2(u) \end{aligned}

如果我们愿意把 f3f_3 也显式地存下来，那么：

f3(p)+=∑u<pf2(u)⇒Ans=∑v=1mf3(v) f_3(p) \mathrel{+}= \sum_{u < p} f_2(u) \quad\Rightarrow\quad \text{Ans} = \sum_{v=1}^m f_3(v)

于是自然得到一个对于任意 ℓ≥2\ell \ge 2 的统一公式：

fℓ(p)+=∑u<pfℓ−1(u) f_\ell(p) \mathrel{+}= \sum_{u < p} f_{\ell-1}(u)

这就是“按长度分层做 DP，按值域用 Fenwick 求前缀和”的核心结构。

2. 推广到任意 k：通用递推公式

对于一般的“长度为 k 的严格上升子序列计数”，我们希望在处理完所有元素之后得到：

Answer=∑v=1mfk(v) \text{Answer} = \sum_{v=1}^{m} f_k(v)

转移规则推广为：

{f1(v)+=1fℓ(v)+=∑u<vfℓ−1(u),2≤ℓ≤k \begin{cases} f_1(v) \mathrel{+}= 1 \\[4pt] f_\ell(v) \mathrel{+}= \displaystyle\sum_{u < v} f_{\ell-1}(u), & 2 \le \ell \le k \end{cases}

每一层对应一个 Fenwick 树：

  • 第 ℓ\ell 层的 Fenwick 维护 fℓ(v)f_\ell(v) 在值域上的前缀和，因此

    ∑u<vfℓ−1(u)=Fenwick_ℓ−1.query(idx−1) \sum_{u < v} f_{\ell-1}(u) = \text{Fenwick}\_{\ell-1}.query(\text{idx}-1)

如果换成“数组写法”的 DP 形式，设

dp[ℓ][v]=fℓ(v), \text{dp}[\ell][v] = f_\ell(v),

那么同样的转移可以写成：

{dp[1][v]+=1,dp[ℓ][v]+=∑u<vdp[ℓ−1][u],2≤ℓ≤k. \begin{cases} \text{dp}[1][v] \mathrel{+}= 1, \\[6pt] \text{dp}[\ell][v] \mathrel{+}= \displaystyle\sum_{u < v} \text{dp}[\ell-1][u], & 2 \le \ell \le k. \end{cases}

再用 Fenwick 把右侧的“前缀和”这一项压缩到 O(log⁡m)O(\log m) 即可。

3. 这里为什么也可以“从前往后滚”？

注意上面的循环顺序（对应我的 INCSEQ 代码）：

1
2
3
4
5
6
7
for (ll p: a) {
    int idx = ...;
    for (int i = 2; i <= k; ++i) {
        update(idx, query(idx - 1, dp_tree[i - 1]), dp_tree[i], size);
    }
    update(idx, 1, dp_tree[1], size);
}

和很多 DP 不同，这里完全不需要从 k → 1 逆序，原因有两点：

  1. 对固定的 len，我们读取的是上一层 dp_tree[len - 1]，
    这一层在当前元素 p 的循环中，还没有被更新过；
  2. 即使在“长度维度”上有前后依赖（例如 len=3 依赖 len=2），
    由于我们只查询 query(idx - 1, dp_tree[len - 1])，
    而当前元素的新贡献只写在 idx 及其后的节点上，
    所以这部分新贡献不会被读到。

Fenwick 树的结构保证：

  • update(idx, ...) 只写 index ≥ idx 的节点；
  • query(idx - 1) 只读 index ≤ idx - 1 的节点。

因此：
从前往后 len=2..k 滚动是绝对安全的，每一层用到的永远都是“上一层在当前元素之前的状态”。

4. 把模板落地：SPOJ INCSEQ

SPOJ INCSEQ - Increasing Subsequences

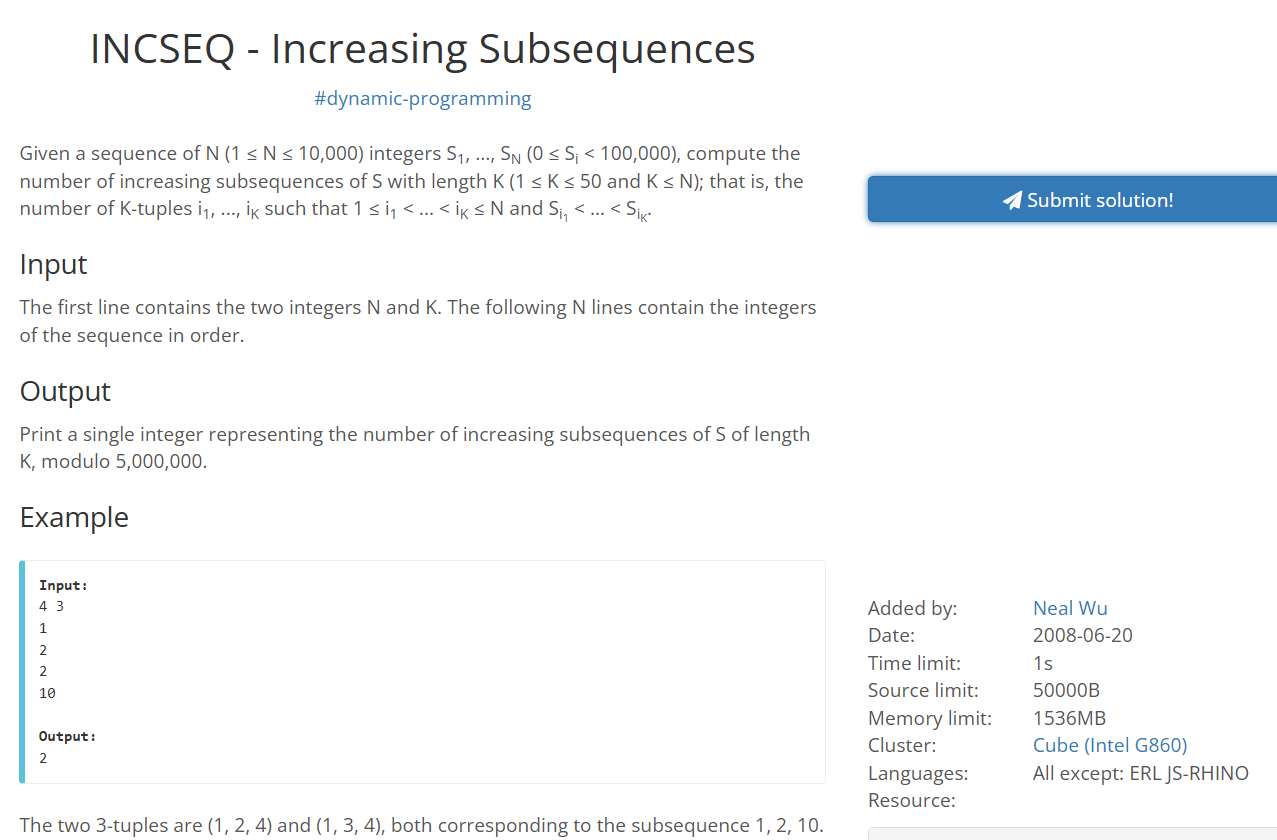
题目大意：给定 nn、kk 和一个长度为 nn 的序列，统计长度恰好为 k 的严格上升子序列个数，对 MOD = 5,000,000 取模。
约束大致为：

  • 1≤n≤1041 \le n \le 10^4
  • 1≤k≤501 \le k \le 50
  • 0≤ai<1000000 \le a_i < 100000

与我们抽象出的模型完全一致，非常适合作为模板题。

5. 实现细节解读

结合我自己的 AC 代码，这里的关键点有几个：

5.1 离散化

仍然通过 coord 进行排序 + 去重，把原始值映射到 [1,size][1, size]：

1
2
3
4
sort(coord.begin(), coord.end());
coord.erase(unique(coord.begin(), coord.end()), coord.end());
int size = (int) coord.size();
int idx = (int) (lower_bound(coord.begin(), coord.end(), p) - coord.begin()) + 1;

这样 Fenwick 的大小只需与 size 相关，而不受原值域限制。

5.2 k 层 Fenwick 的组织方式

使用一个二维数组：

1
vector<vector<ll> > dp_tree(k + 5, vector<ll>(size + 5, 0));

这里的含义是：

  • dp_tree[len] 是“长度为 len 的那一层 Fenwick 树内部数组”；
  • dp_tree[len][pos] 就是 fℓ(v)f_\ell(v) 在树状数组上的内部节点。

配合 update / query 函数，这就形成了 k 层树状数组结构。

5.3 模运算

代码里所有加法都通过

1
2
tree[i] = (tree[i] + val) % MOD;
sum = (sum + tree[i]) % MOD;

保持在 [0,MOD)[0, \text{MOD}) 内，防止溢出；
同时题目需要对 5,000,000 取模，这里直接在 Fenwick 的每一步更新里处理掉。

5.4 复杂度

对于每个元素 p：

  • 需要对 len = 2..k 做一次 query + update，每次是 O(log⁡size)O(\log size)；
  • 再对 len = 1 做一次 update。

整体时间复杂度：

O(n⋅k⋅log⁡n) O\left(n \cdot k \cdot \log n\right)

在 n=104,k≤50n = 10^4, k \le 50 的条件下是完全没压力的。

6. INCSEQ 最终 AC 代码

这份代码是我在 SPOJ 上 AC 的版本，用的正是上面抽象出的模板思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll maxn = 1e4 + 5, MOD = 5000000;

ll n, k;
vector<ll> a, coord;

int lowbit(int x) {
    return x & -x;
}

void update(int idx, ll val, vector<ll> &tree, int limit) {
    for (int i = idx; i <= limit; i += lowbit(i)) {
        tree[i] = (tree[i] + val) % MOD;
    }
}

ll query(int idx, const vector<ll> &tree) {
    ll sum = 0;
    for (int i = idx; i; i -= lowbit(i)) {
        sum = (sum + tree[i]) % MOD;
    }
    return sum;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    a.reserve(maxn);
    coord.reserve(maxn);
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) {
        ll num;
        cin >> num;
        a.push_back(num);
        coord.push_back(num);
    }
    sort(coord.begin(), coord.end());
    coord.erase(unique(coord.begin(), coord.end()), coord.end());
    int size = (int) coord.size();
    vector<vector<ll> > dp_tree(k + 5, vector<ll>(size + 5, 0));
    for (ll p: a) {
        int idx = (int) (lower_bound(coord.begin(), coord.end(), p) - coord.begin()) + 1;
        for (int i = 2; i <= k; ++i) {
            update(idx, query(idx - 1, dp_tree[i - 1]), dp_tree[i], size);
        }
        update(idx, 1, dp_tree[1], size);
    }
    cout << query(size, dp_tree[k]);
    return 0;
}

（另一些做题时的草稿）

总结：可以直接收进代码库的结论

用一句话概括这篇文章要留下的东西，就是这组状态转移：

{f1(v)+=1,fℓ(v)+=∑u<vfℓ−1(u),2≤ℓ≤k. \begin{cases} f_1(v) \mathrel{+}= 1, \\[6pt] f_\ell(v) \mathrel{+}= \displaystyle\sum_{u < v} f_{\ell-1}(u), & 2 \le \ell \le k. \end{cases}

如果换成数组写法，设

dp[ℓ][v]=fℓ(v), \text{dp}[\ell][v] = f_\ell(v),

则等价的 DP 形式是：

{dp[1][v]+=1,dp[ℓ][v]+=∑u<vdp[ℓ−1][u],2≤ℓ≤k. \begin{cases} \text{dp}[1][v] \mathrel{+}= 1, \\[6pt] \text{dp}[\ell][v] \mathrel{+}= \displaystyle\sum_{u < v} \text{dp}[\ell-1][u], & 2 \le \ell \le k. \end{cases}

再用 Fenwick 把右侧的「前缀和」这一项压缩到 O(log⁡m)O(\log m)，就得到一套：

  • 时间复杂度 O(n⋅k⋅log⁡n)O(n\cdot k \cdot \log n)；
  • 支持任意 kk 的严格上升子序列计数；
  • 可以轻松套在不同题目上的通用模板。

P1637 是这套模板在 k=3k=3 情况下的“特例写法”；
INCSEQ 则是把这个结构完整展开的一道标准模板题。

后面如果再遇到“长度为 k 的严格上升子序列”相关题目，可以直接在这份代码基础上做修改和扩展，而不需要重新从头推思路。